Моменты инерции сечений сложной формы

Момент инерции сечения сложной формы относительно некоторой оси равен сумме моментов инерций его составных частей относительно той же оси:

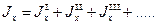, (3.30)

что непосредственно следует из свойств определенного интеграла. Таким образом, для вычисления момента инерции сложной фигуры необходимо разбить её на ряд простых фигур, вычислить моменты инерции этих фигур, а затем просуммировать их.

Пусть требуется определить моменты инерции сложной фигуры относительно осей X, Y (рис. 3.11). При вычислении моментов инерции сложных сечений их нужно разбить на простые части, моменты инерции которых известны.

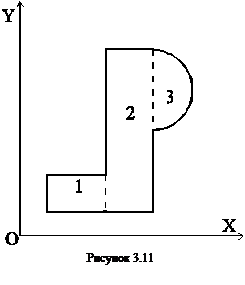Из основного свойства интеграла суммы следует, что момент инерции сложной фигуры равен сумме моментов инерции составных ее частей:

;

.

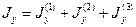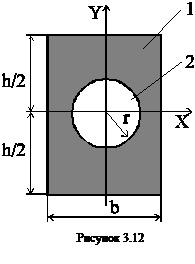
Если в сечении имеется отверстие (рис. 3.12), то его удобно считать фигурой с отрицательной площадью:

;

.

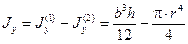3.10 Стандартные прокатные профили

Нашей промышленностью выпускаются стандартные прокатные профили (рис. 3.13) (двутавр, швеллер, уголок равнобокий, уголок неравнобокий), которые могут быть использованы как готовые элементы конструкций (балки, стойки, элементы ферм и т.д.). Размеры прокатных профилей стандартизированы и сведены в таблицы сортаментов прокатной стали, которые приводятся в приложениях почти всех учебников и сборников задач по сопротивлению материалов. В этих таблицах приводятся все размеры сечений и основные геометрические характеристики прокатных профилей в соответствии с их номером.

двутавр	швеллер	Равнобокий уголок	неравнобокий уголок

Рисунок 3.13

Дата добавления: 2015-06-28