Плоское напряженное состояние

Линейное напряженное состояние

Линейным или одноосным называется напряженное состояние, при котором два из трех главных напряжений равны нулю (рис. 4.2, в).

Определим напряжения, возникающие в наклонном сечении АВ (рис. 4.3), нормаль к которому повернута на угол a к направлению s₁.

За положительное направление отсчетов угла a примем направление против часовой стрелки.

В общем случае в наклонном сечении будут действовать как нормальные напряжения s_a, так и касательные напряжения t_a.

Их значения определим из условия равновесия нижней части.

Проектируя силы на направления s_a, имеем:

учитывая, что

получаем .

Из суммы проекций сил на направления t_a имеем:

Плоским или двухосным называется напряженное состояние, при котором одно из трех главных напряжений равно нулю (рис. 4.2,б).

Для плоского напряженного состояния различают две задачи – прямую и обратную. В прямой задаче гранями рассматриваемого элемента являются главные площадки (рис. 4.4,а). Известны s₁ ¹ 0, s₂ ¹ 0, s₃ = 0 и требуется определить напряжения s_a и t_a и s_b и t_b на произвольных площадках. В обратной задаче известны напряжения на двух взаимно произвольных перпендикулярных площадках s _х, s _y, t _yx, t _xy и требуется определить положение главных площадок и величины главных напряжений.

Прямая задача. Для решения этой задачи воспользуемся принципом независимости действия сил. Представим плоское напряженное состояние в виде суммы двух независимых линейных напряженных состояний: первое – при действии только напряжений s₁, второе – при действии только напряжений s₂. От каждого из напряжений s₁ и s₂ напряжения s_aи t_a в произвольной площадке равны:

d F

Рисунок 4.4

Таким образом, суммируя напряжения, возникшие при каждом линейном напряженном состоянии, получим:

Определим напряжения, действующие на площадку с углом наклона , то есть перпендикулярную к площадке a:

Суммируя нормальные напряжения, действующие по произвольным взаимно перпендикулярным площадкам, получим:

Сравнивая величины касательных напряжений, имеем .

Таким образом, касательные напряжения достигают наибольшей величины при a = ± 45°, т.е. к площадкам наклоненным к главным площадкам под углом 45°, причем:

.

Обратная задача. Определим сначала напряжения на наклонной площадке, наклоненной к исходной, при заданныхнапряжения на двух взаимно произвольных перпендикулярных площадках s _x, s _y, t _yx и t _xy (рис. 4.4,б).

Разрежем параллелепипед плоскостью, наклоненной под углом a к вертикальной грани, отбросим левую часть и рассмотрим равновесие правой части.

Если обозначить через площадь наклонной грани, то площади вертикальной и горизонтальной граней будут соответственно равны 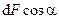и .

Спроектируем силы на направления s_a и t_a:

Сокращая на и учитывая, что , получаем:

Для отыскания экстремального значения нормального напряжения продифференцируем s_a по a:

Экстремум напряжения s_a достигается при тех углах a, при которых 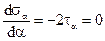. Отсюда следует, что нормальные напряжения достигают экстремума на тех площадках, где касательные ускорения обращаются в нуль. Эти площадки называются главными, а напряжения, возникающие на них – главными напряжениями.

Предполагая, что главные площадки наклонены к исходным площадкам на угол a₀, получаем:

.

Полученному равенству удовлетворяют два значения угла a₀, отличающиеся на 90°. Таким образом, данная формула определяет две взаимно перпендикулярные площадки, на которых нормальные напряжения принимают экстремальные значения. Учитывая, что сумма нормальных напряжений по двум взаимно перпендикулярным площадкам постоянна, то на одной площадке будет действовать максимальное нормальное напряжения, а по другой – минимальное.

Модули главных напряжений определяют по зависимости:

.

Дата добавления: 2015-06-28