Напряжения в поперечном сечении

Рассматривая кручение вала, легко установить, что под действием скручивающего момента любое сечение на расстоянии х от заделки поворачивается относительно закрепленного сечения на некоторый угол j - угол закручивания (рис. 6.2). При этом чем больше скручивающий момент M_к, тем больше и угол закручивания. Зависимости 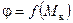, называемые диаграммами кручения, полученные для образца из пластичного материала, до некоторой степени подобны диаграммам растяжения (рис. 6.3). В дальнейшем при выводе формул для напряжений и угла закручивания нас будет интересовать участок диаграммы кручения, соответствующий работе материала в пределах пропорциональности.

Рассмотрим геометрическую картину деформации вала при кручении.

Если до деформации на поверхность вала нанести сетку, состоящую из линий, параллельных оси, и линий, представляющие собой параллельные круги, то после закручивания вала скручивающим моментом M_к можно заметить следующее: образующие цилиндра превращаются в винтовые линии, параллельные круги не искривляются и расстояние между ними остается неизменным, радиусы, проведенные в торцевых сечениях остаются прямыми (рис. 6.4).

Полагая, что картина, наблюдаемая на поверхности вала, сохраняется и внутри, сформулируем гипотезы, взятые в основу теории кручения круглых стержней:

1. Поперечные сечения, плоские и нормальные к оси вала до деформации, остаются плоскими и нормальными к той же оси и после деформации.

2. Прямолинейная ось вала остается прямолинейной и после деформации, а все поперечные сечения поворачиваются вокруг этой оси по отношению друг к другу на какой то угол dj.

3. Радиусы поперечных сечений при деформации не искривляются.

4. Расстояния между сечениями вала в процессе деформации не изменяются, следовательно, и вся длина вала остается прежней.

На основании принятых гипотез кручение круглого вала можно представить как результат сдвигов, вызванных взаимным поворотом поперечных сечений относительно друг друга. Вследствие этого в поперечных сечениях возникают только касательные напряжения, а нормальные напряжения равны нулю.

Выделим из закручиваемого вала диск радиуса r на расстоянии x от закрепленного конца, ограниченный двумя смежными сечениями m-m и n-n, находящимися друг от друга на расстоянии d x (рис. 6.5) и рассмотрим его отдельно.

Если сечение m-m, лежащее на расстоянии x от защемленного конца вала, повернулось относительно последнего на угол j, то сечение n-n, находящееся на расстоянии 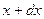, повернется относительно закрепленного конца на угол .

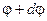Точк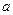и и 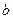до деформации лежащие на одной образующей, после деформации расположатся на винтовой линии и займут новое положение a ¢ и b ¢.

Проведем от точки a прямую ab ², параллельную a ¢ b ¢ и соединим центр сечения n-n с точкой b ². Тогда угол bOb ², равный d j, будет углом поворота сечения n-n относительно сечения m-m. У элемента ab ² b ¢ a ¢ до поворота сечения n-n относительно сечения m-m верхняя и нижняя стороны были расположены горизонтально. После поворота стороны наклонились и приняли положение ab ² и a ¢ b ¢. Следовательно, элемент претерпел абсолютный сдвиг, равный длине дуги:

.

Относительный сдвиг будет равен:

.

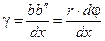Отношение 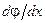представляет относительный угол закручивания q (угол закручивания на единицу длины бруса). Тогда

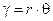. (6.1)

Из этой формулы видно, что относительный сдвиг пропорционален радиусу закручиваемого цилиндрического тела.

На основании закона Гука для сдвига:

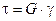. (6.2)

Можно определить касательное напряжение для элементов лежащих на поверхности вала:

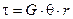. (6.3)

Учитывая предположение, что деформация элементов на поверхности вала подобна деформации элементов внутри вала, для произвольного элемента, находящегося на расстоянии r от центра поперечного сечения (рис 6.6):

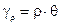, (6.4)

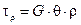. (6.5)

Касательная элементарная сила на площадке d F расположенной на расстоянии r от оси вала:

.

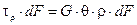Момент элементарной силы относительно оси бруса будет:

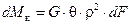. (6.6)

Сумма таких элементарных моментов, распределенных по всему поперечному сечению F, при равновесии, наступающем после деформации, должна быть равна крутящему моменту:

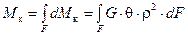. (6.7)

Вынесем постоянные за знак интеграла, получим:

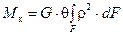. (6.8)

Интеграл 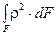является полярным моментом инерции J _r. Тогда

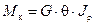. (6.9)

Откуда относительный угол закручивания:

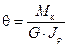. (6.10)

Подставляя в выражение (6.5) выражение относительного угла закручивания получим

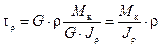. (6.11)

Это уравнение показывает, что напряжения в площадках сечения прямо пропорциональны их расстояниям до центра сечения.

Анализируя эпюру касательных напряжений (рис. 6.6) можно отметить, что наибольшие напряжения возникают на поверхности вала, в центральной части они значительно меньше и на продольной оси равны нулю. Следовательно, в сплошном валу материал, находящийся в центральной части в значительной степени недогружен, его вклад в прочность вала мал. Поэтому рациональным для валов считается кольцевое сечение.

Дата добавления: 2015-06-28