Пример 3. Рассмотрим двухопорную балку (рис

Рассмотрим двухопорную балку (рис. 8.8, а). На балку действует в точке C сосредоточенный момент 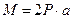, в точке D - сосредоточенная сила P и на участке BD - равномерно распределенная нагрузка интенсивностью .

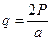Определим опорные реакции и 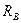(рис. 8.8, б). Равнодействующая распределенной нагрузки равна 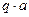, а линия действия ее проходит через центр участка BD. Составим уравнения моментов относительно точек B и A:

;

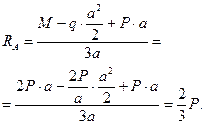
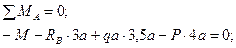
Определим поперечную силу и изгибающий момент в произвольном сечений, расположенном на участке AC на расстоянии x ₁ от точки А (рис. 8.8, в). Расстояние x ₁ может изменяться в пределах ().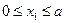

.

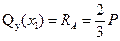Значение поперечной силы не зависит от координаты сечения x ₁, следовательно, во всех сечениях участка AC поперечные силы одинаковы и эпюра 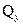имеет вид прямоугольника.

Изгибающий момент изменяется по линейному закону:

.

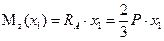Для построения эпюры вычисляем ординаты на границах участка.

при :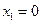

.

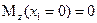при :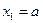

.

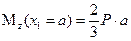Определим поперечную силу и изгибающий момент в произвольном сечений, расположенном на участке CB на расстоянии x ₂ от точки C (рис. 8.8, г). Расстояние x ₂ может изменяться в пределах ().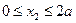

.

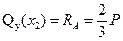Значение поперечной силы не зависит от координаты сечения x ₂, следовательно, во всех сечениях участка CB поперечные силы одинаковы и эпюра 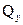имеет вид прямоугольника. Изгибающий момент:

.

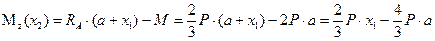Изгибающий момент изменяется по линейному закону. Определим ординаты эпюры для границ участка:

;

.

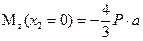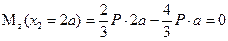Определим поперечную силу и изгибающий момент в произвольном сечений, расположенном на участке BD на расстоянии x ₃ от точки D (рис. 8.8, д). Расстояние x ₃ может изменяться в пределах ().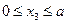

.

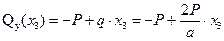Поперечная сила изменяется по линейному закону. Определим для границ участка.

;

.

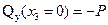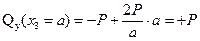Изгибающий момент:

.

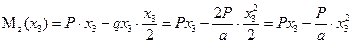Эпюра изгибающих моментов на этом участке будет параболической.

;

.

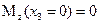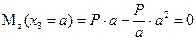Чтобы определить экстремальное значение изгибающего момента, приравниваем к нулю производную от изгибающего момента по абсциссе сечения x ₃:

.

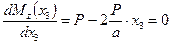Отсюда

.

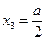Для сечения с координатой 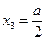значение изгибающего момента будет составлять

.

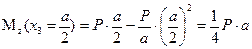В результате получаем эпюры поперечных сил (рис. 8.8, е) и изгибающих моментов (рис. 8.8, ж).

Дата добавления: 2015-06-28