Построение эпюр поперечной силы и изгибающего момента

Рассмотрим балку длиной l защемленную одним концом и находящуюся под действием сосредоточенной силы Р (рис. 8.3). Пусть для определенности Р = 4 кН, l = 2 м.

Определим внутренние силовые факторы, возникающие в балке. Воспользуемся методом сечением.

Рассечем балку поперечным сечением в произвольном месте.

Отбросим правую часть.

Заменим ее действие внутренними усилиями N - вдоль оси z, Q_y - вдоль оси y и моментом M_x – в плоскости осей yz вокруг оси х. На рис. 8.3 в соответствии с принятым правилом знаков показаны положительные направления внутренних силовых факторов.

Уравновесим отсеченную часть. Запишем уравнения статического равновесия, получим:

Из первого уравнения видно, что нормальная сила N при изгибе равна нулю, далее не будем ее определять.

Построим эпюры поперечной силы Q_y и изгибающего момента M_x вдоль длины балки.

Поперечная сила постоянна по всей длине балки и равна Q_y = P = 4 кН. Отложим на графике линию параллельную оси z.

Изгибающий момент М_х изменяется в зависимости от расстояния z. Вычислим его значение в двух точках: в начале z = 0 и в конце балки z = l = 2 м.

z = 0, М_х = 0;

z = 2 м, М_х = 8 кНм.

Построим по точкам график М_х.

Построение эпюр поперечной силы Q_y и изгибающего момента M_x является одним из основных этапов при расчете конструкций на изгиб. По эпюрам Q_y и M_x определяется опасное сечение, т.е. сечение в котором может произойти разрушение.

Опасным сечением называется сечение, в котором изгибающий момент достигает наибольшего по модулю значения .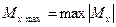

В некоторых случаях опасным сечением может быть также сечение, где наибольшего значения достигает поперечная сила 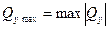. В данном случае опасным является место закрепления балки.

Рассмотрим примеры построения эпюр Q_y и M_x.

Пример 1:

z₁

Для балки, изображенной на рис. 8.4 построить эпюры поперечной силы Q_y и изгибающего момента M_x и определить опасное сечение. Пусть величины P = 10 кН, a = 2 м, b = 3 м.

Решение.

Определим реакции опор. Запишем уравнения равновесия статики. Из этих уравнений получим:

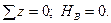
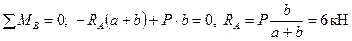
Для проверки правильности определения реакции опор используем уравнение:

® 6 – 10 + 4 = 0, ® 0 º 0.

Значит, реакции определены правильно.

Определим внутренние усилия, возникающие в материале балки. Следует рассмотреть два участка, границами участков являются точки приложения сосредоточенной силы Р и опорных реакций R_A и R_B. Обозначим границы участков буквами А, С и В.

Рассечем первый участок АС.

Отбросим правую часть, т.к. она сложнее.

Заменим отброшенную часть внутренними усилиями Q_y и M_x.

Уравновесим отсеченную часть, запишем уравнения равновесия:

Вычислим Q_y и M_x в граничных точках участка:

при z ₁ = 0, Q_{y 1} = R_A = 6 кН, M_{x 1} = 0;

при z ₁ = а = 2 м, Q_{y 1} = R_A = 6 кН, M_{x 1} = 12 кН×м.

Рассмотрим второй участок СВ. Рассечем его и отбросим левую часть, заменим её внутренними силами. Из уравнений равновесия получим:

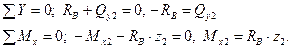
Вычислим Q_y и M_x в граничных точках участка:

при z ₂ = 0, Q_{y 2} = - R_В = - 4 кН, M_{x 2} = 0;

при z ₂ = а = 3 м, Q_{y 2} = - R_В = - 4 кН, M_x2 = 12 кН×м.

Построим эпюры Q_y и M_x.

По полученным эпюрам определим опасное сечение, оно проходит через точку приложения силы P, так как M_x достигает там наибольшего значения.

Пример 2: Для представленной на рис. 8.5 балки построить эпюры внутренних сил, найти опасные сечения.

Решение.

Определим реакции опор. Заменим распределенную нагрузку q её равнодействующей G = 2 qa, приложим G в середине участка АС (рис. 8.6).

Запишем уравнение равновесия.

Отсюда находим:

Выполним проверку правильности определения реакций опор:

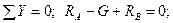® ;® 0 º 0.

Используя метод сечений, рассмотрим сечения участков балки (рис. 8.7).

1 участок:

Вычислим Q_{y 1} и M_{x 2} на границах участка:

2 участок:

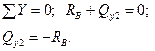
На границах участка получим:

Построим эпюры Q_y и M_x на участках. Из выражений для внутренних усилий следует, что Q_y, эпюра является прямолинейной как на первом, так и на втором участках, в то время как эпюра М_х на первом участке квадратичная парабола, а на втором прямая линия. Для построения эпюры М_х на первом участке следует либо вычислить её значения в нескольких точках, либо исследовать функцию на экстремум и определить его.

Как известно из курса математического анализа, для определения экстремума функции следует определить ее первую производную, приравняв ее нулю найти аргумент, затем его значение подставить в функцию и вычислить экстремум функции:

,

.

Отложим значение М_{х max} и построим эпюру изгибающего момента на первом участке по трем точкам (рис. 8.7).

По эпюре находим опасное сечение. Им является сечение, где .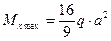

Дата добавления: 2015-06-28