Решение и обсуждение результатов

Постановка задачи.

Точечный заряд 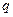расположен на расстоянии 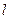от центра металлической заземленной сферы радиуса 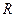. Построить картину силовых линий поля, распределение потенциала в плоскости, содержащей заряд и центр сферы. Найдите: суммарный индуцированный заряд сферы; силу взаимодействия заряда и сферы.

На поверхности металлической заземленной сферы возникнут индуцированные заряды, распределение которых заранее не известно, однако потенциал сферы равен нулю. В предыдущем разделе мы показали, что поле двух точечных зарядов имеет в качестве поверхности нулевого потенциала сферу. Теперь мы можем использовать этот результат.

Для этого необходимо внутри сферы построить заряд изображение 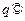, такой, чтобы поле двух точечных зарядов имело нулевой потенциал на поверхности сферы. В этом случае вне сферы поле двух точечных зарядов 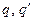и поле, создаваемое зарядом 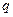и зарядами, индуцированными на поверхности металлической сферы, будут одинаковыми. (Вне сферы распределения зарядов одинаковы, на границе - одинаковые граничные условия).

Для определения величины заряда-изображения 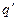и его положения можно, конечно, воспользоваться полученным ранее уравнением, однако проще потребовать выполнения условия 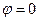в двух точках сферы 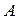и 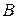(рис. 17):

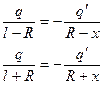; (22)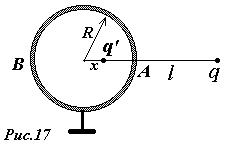

Решив эту систему относительно неизвестных 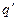и 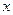, получим

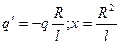. (23)

Таким образом, поле вне сферы эквивалентно полю двух точечных зарядов. Внутри сферы эти поля, конечно же, различаются - внутри реальной проводящей сферы поле отсутствует.

На рис.18 показаны силовые линии поля, при двух различных значениях расстояния до точечного заряда. Обратите внимание, что при увеличении расстояния между зарядом и сферой искажения поля точечного заряда уменьшаются. Как всегда, у поверхности проводника силовые линии перпендикулярны границе, что соответствует условию равновесия индуцированных зарядов на поверхности проводника.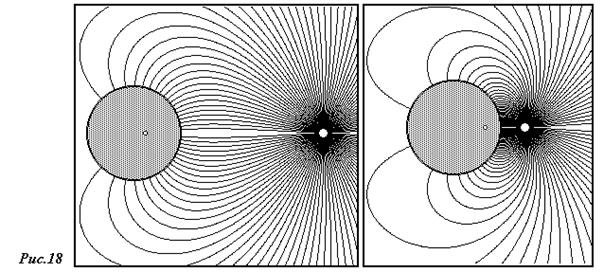

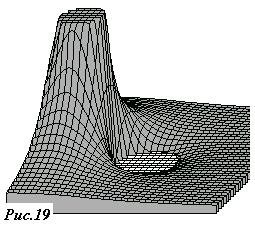Достаточно интересна поверхность, иллюстрирующая распределение потенциала (рис.19). Так как сфера заземлена, то на ее поверхности и внутри нее потенциал равен нулю, что хорошо видно на рисунке.

Замечу, что функция, описывающая потенциал поля, вне сферы совпадает с потенциалом поля точеного заряда, а внутри сферы равна нулю - именно таким образом она и была определена в программе, выполнившей построение этого рисунка. Также напомню, что резкое «возвышение» есть потенциал поля точечного заряда, который стремится к бесконечности, здесь как и на других рисунках он «обрезан».

Для определения суммарного индуцированного заряда воспользуемся теоремой Гаусса. Окружим сферу замкнутой поверхностью. По теореме Гаусса, поток вектора напряженности электрического поля через эту поверхность равен суммарному заряду внутри поверхности, деленному на 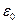. Так поле индуцированных зарядов эквивалентно полю заряда изображения, то и суммарный индуцированный заряд равен величине заряда-изображения.

Еще раз подчеркну - вне сферы поля эквивалентны, но это не значит, что индуцированные заряды концентрируются в одной точке - они распределены по поверхности сферы.

Силу взаимодействия между сферой и точечным зарядом м 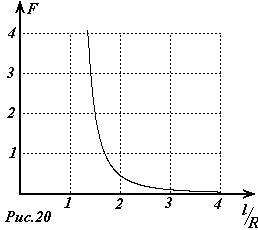ожно найти как силу взаимодействия между двумя точечными зарядами :

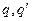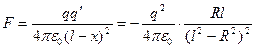(24).

График этой функции представлен на рис.20 (где сила выражена в относительных единицах - в таковых, что 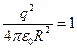). При 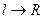сила взаимодействия возрастает до бесконечности.

Заметим, что при 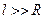формула (24) дает

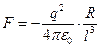, (25)

то есть сила убывает обратно пропорционально кубу расстояния. Такая зависимость может быть качественно объяснена: величина заряда, индуцированного на сфере обратно пропорциональна расстоянию до исходного заряда, а сила взаимодействия между точечными зарядами обратно пропорциональна квадрату расстояния - следовательно, сила взаимодействия сферы и заряда обратно пропорциональна кубу расстояния.

Задание для самостоятельной работы.

1. Использованный метод построения изображения в сфере применим и в том случае, если заряд находится внутри сферы - тогда изображение окажется снаружи. Постройте картину силовых линий поля для заряда находящегося внутри сферы.

Рассмотрим, как изменится картина поля, если сфера не заземлена. Если сфера не заземлена, то потенциал ее отличен от нуля, но по-прежнему постоянен. Таким образом, граничное условие изменяется - потенциал сферы постоянен, но не известно чему он равен. Однако, для изолированной сферы суммарный индуцированный заряд равен нулю - в поле точечного заряда произойдет перераспределение зарядов по поверхности сферы. Мы можем легко добиться выполнения граничных условий поместив в центр шара еще один заряд-изображение (рис.21) 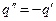. 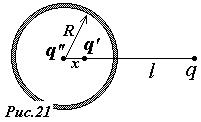В этом случае эквипотенциальность сферы не нарушится, а ее суммарный заряд останется равным нулю.

Итак, вне сферы поле, создаваемое точечным зарядом 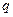и индуцированными зарядами на поверхности, эквивалентно полю трех точечных зарядов 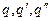. Построить силовые линии такого поля не представляет труда, особенно, если имеется программа для расчета поля с заземленной сферой - достаточно добавить еще одно слагаемое, описывающее поле второго заряда изображения. Результаты таких расчетов показаны на рис.22.

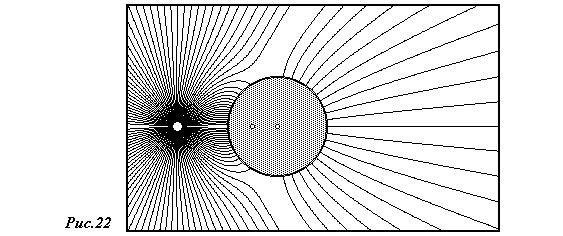В этом случае, помимо силовых линий, начинающихся на исходном заряде, построены линии, начинающиеся на положительных индуцированных зарядах на сфере. Незаземленная сфера гораздо меньше возмущает поле, чем заземленная. Действительно, на ней происходит только перераспределение зарядов.

Суммарный заряд сферы останется равным нулю, но сфера приобретет индуцированный дипольный момент, который равен дипольному моменту двух зарядов-изображений

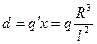. (26)

Сила, действующая на заряд 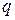также легко вычисляется

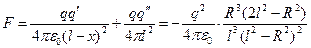. (27)

При 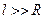сила взаимодействия

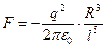, (28)

убывает обратно пропорционально пятой степени расстояния, что также легко объяснимо: величина индуцированного дипольного момента пропорциональна величине внешнего поля (которое убывает обратно пропорционально квадрату расстояния), а величина поля диполя убывает обратно пропорционально кубу расстояния.

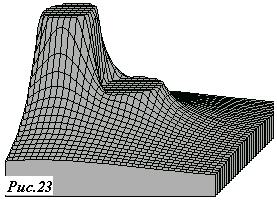
Посмотрите также на распределение потенциала в плоскости, проходящей через заряд и центр сферы (рис.23). В этом случае потенциал сферы постоянен и больше нуля.

Кстати, легко можно вычислить потенциал сферы, не рассчитывая распределения зарядов на поверхности. По принципу суперпозиции, потенциал центра сферы равен сумме потенциалов заряда 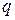и индуцированных зарядов на поверхности сферы. Все индуцированные заряды находятся на одном и том же расстоянии от центра и их сумма равна нулю, следовательно, равен нулю и потенциал, создаваемый ими в центре сферы. Поэтому потенциал в центре сферы, а следовательно и в любой ее точке, равен потенциалу поля точечного заряда .

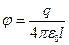Задания для самостоятельной работы.

1. Постройте график зависимости силы взаимодействия незаземленной сферы и точечного заряда от расстояния между ними. Определите, при каких расстояниях можно пользоваться приближенной формулой (28), вместо более сложной (27). Условия применимости сформулируйте самостоятельно.

2. Пусть металлическая сфера несет некоторый заряд. При определенных условиях сфера может притягивать точечный заряд того же знака. Найдите эти условия.

Дата добавления: 2015-06-28