Суждения

Термин считается распределенным, если он взят в полном объеме. Термин считается нераспределенным, если он взят в части объема. Распределенность термина можно выразить в круговых схемах и в таблице (табл.1).

Таблица 1

Распределенность терминов в простых невыделяющих и выделяющих суждениях

Вид суждения   Термины	A	E	I	O
S	+	+	-	-
P	-	+	-	+
P выделяющих суждений	+	+	+	+

Таблицы истинности позволяют устанавливать логическое значение суждения (истинность, ложность) в зависимости от значений, образующих его суждений.

Число всех возможных наборов значений n переменных равно , что соответствует числу строк в соответствующей таблице.

Составим комплексную таблицу истинности для суждений, образованных следующими логическими союзами: 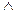– конъюнкция, – дизъюнкция, 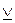– строгая дизъюнкция, 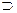– материальная импликация, – материальная эквиваленция, 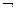– отрицание (табл.2).

Таблица 2

Таблица истинности высказываний

A	B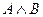
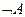
и	и	и	и	л	и	и	л
л	и	л	и	и	и	л	и
и	л	л	и	и	л	л
л	л	л	л	л	и	и

Запись суждений в языке логики предикатов:

– общеутвердительное суждение (A),

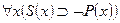– общеотрицательное суждение (E),

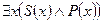– частноутвердительное суждение (I),

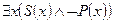– частноотрицательное суждение (O).

ДЕДУКТИВНЫЕ УМОЗАКЛЮЧЕНИЯ

Непосредственные умозаключения (превращения, обращения, противопоставления предикату). Непосредственными называют такие умозаключения, вывод в которых получен логическим преобразованием одной посылки.

Превращение – преобразование суждения в противоположное по качеству с предикатом, противоречащим предикату исходного суждения.

Схемы превращения: , где S, P – термины субъекта и предиката суждения; a,e,i,o – обозначения для общеутвердительного, общеотрицательного, частноутвердительного, частноотрицательного суждений; P’ – противоречащее понятие.

Обращение - преобразование суждения, в котором субъект и предикат исходного суждения в заключении меняются местами.

Схемы обращения с ограничением: .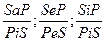

Обращение без ограничения для выделяющих суждений: .

Примечание: Частноотрицательные суждения (O) не обращаются.

Противопоставление предикату - преобразование суждения, в результате которого субъектом заключения становится понятие, противоречащее предикату исходного, а предикатом его субъект.

Схемы противопоставления предикату: .

Примечание: Частноутвердительные суждения (I) противопоставлением предикату не преобразуются.

Опосредованные умозаключения. Простой категорический силлогизм (ПКС). ПКС - это умозаключение, в котором заключение следует из двух посылок, называемых большей и меньшей. Содержащийся в обеих посылках средний термин (M) связывает два крайних термина: больший (P) и меньший (S). Меньший термин становится субъектом заключения, а больший его предикатом.

Фигурой называется порядок употребления в ПКС большего, меньшего и среднего терминов. В формальной логике выделяют четыре фигуры. Модусом называют типы простых суждений (A, E, I, O), употребляемых в качестве посылок в фигурах. Всего возможны 256 модусов по всем четырем фигурам и по 64 модуса в каждой из фигур. Из них выделяют две группы модусов правильные (заключающие) и неправильные (незаключающие). Заключающим называют модус, вывод в котором истинный вывод с необходимостью следует из истинных посылок. Большинство авторов выделяют 19 модусов такого рода. Незаключающим называют модус не гарантирующий истинного вывода из истинных посылок. Заключающие модусы ПКС сведены в табл.3.

Аксиома силлогизма. Все, что утверждается (или отрицается) относительно всех предметов класса, то утверждается (или отрицается) относительно любого отдельного предмета и любой части предметов этого класса.

Таблица 3

Дата добавления: 2015-06-28