Замена плоскостей проекций

Общие сведения

В рассмотренных задачах определялось взаимное расположение в пространстве геометрических фигур. Такие задачи называют позиционными.

В практике встречаются задачи, в которых требуется определить истинную величину, например, отрезка, угла и др. Такие задачи называют метрическими.

Для того чтобы найти истинную величину фигуры, ее располагают параллельно одной из плоскостей проекций. При этом фигуру можно перевести из общего положения в частное либо вращением самой фигуры, либо заменой положения плоскостей проекций (H и V).

Необходимо заметить, что эти способы применяют не только для определения истинных величин фигур, но и с целью упрощения решения задач.

Сущность способа замены плоскостей проекций заключается в том, что при неизменном положении объекта в пространстве производится замена данной системы плоскостей проекций новой системой взаимно перпендикулярных плоскостей проекций (рис. 103).

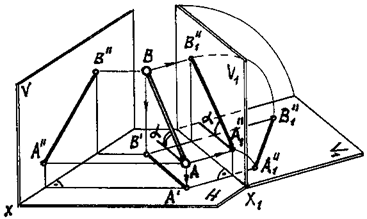
Рис. 103

При переходе к новой системе одну из плоскостей проекций заменяют новой таким образом, чтобы данный геометрический элемент (прямая, плоскость) занял частное положение и проецировался без искажения.

При решении ряда задач, например, требуется преобразовать прямую общего положения в прямую уровня, а затем — в проецирующую, выполнив при этом последовательно два преобразования.

Рассмотрим ход решения этой задачи.

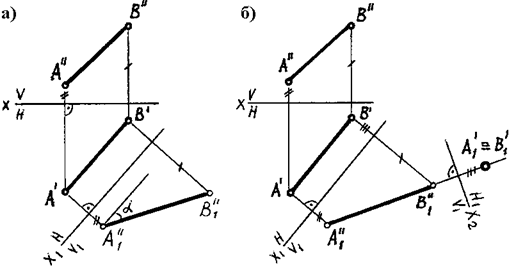
Рис. 104

1 ПРЕОБРАЗОВАНИЕ (рис. 104,а). Для того, чтобы прямая АВ стала линией уровня, следует ввести новую плоскость проекций и расположить ее параллельно данной прямой. При этом новая ось x ₁ будет параллельна одной из проекций прямой. Проведем ось параллельно горизонтальной проекции АВ. Новая плоскость проекций V₁ расположится параллельно прямой АВ, которая проецируется на эту плоскость в истинную величину*

Правило: при замене плоскостей проекций расстояние от новой проекции точки до новой оси равно расстоянию от заменяемой проекции точки до старой оси проекций.

Иными словами, высоты (аппликаты) концов отрезка в новой системе плоскостей проекций останутся прежними. В результате этой замены решена задача на определение действительной величины отрезка и угла наклона a к плоскости H. На чертеже плоскость V₁ совмещают с плоскостью H.

2 ПРЕОБРАЗОВАНИЕ (рис. 104,á). Для того, чтобы прямая АВ оказалась проецирующей, т.е. изобразилась точкой, необходимо произвести вторую замену плоскости проекций и расположить новую плоскость H₁ перпендикулярно прямой. Новую ось x ₂ располагаем перпендикулярно новой фронтальной проекции прямой А" ₁ В" ₁. На новой плоскости проекций Н₁ прямая изобразится точкой, так как координаты концов отрезка в системе Н/V₁ одинаковы.

Таким образом, прямая АВ в системе H₁/V₁ стала проецирующей относительно плоскости H₁. Преобразования в этой задаче могли быть выполнены и в другой последовательности: сначала могла быть заменена горизонтальная плоскость проекций, а затем — фронтальная.

Рассмотрим еще одну задачу — требуется определить истинную.

величину плоской фигуры — треугольника АВС, занимающего в пространстве общее положение. Для решения этой задачи необходимо преобразовать чертеж (эпюр) так, чтобы плоскость общего положения стала параллельной одной из плоскостей проекций новой системы*.

Сначала заменим фронтальную плоскость проекций новой плоскостью V₁, перпендикулярной плоскости треугольника. Это условие выполнено с помощью вспомогательной прямой — линии уровня (горизонталь AN) (рис. 105). Новая ось x ₁ проводится перпендикулярногоризонтальной проекции горизонтали. На новой плоскости проекций V₁ горизонталь спроецировалась в точку, а плоскость треугольника — в линию. Угол a определяет угол наклона треугольника к горизонтальной плоскости H.

Рис. 105

На втором этапе решения задачи проводим вторую замену — новую плоскость проекций H₁ устанавливаем параллельно треугольнику. Новóю ось x ₂ проводим параллельно новой фронтальной проекции треугольника — прямой b ₁ a ₁ c ₁. Построенная проекция определяет истинную величину и форму треугольника.

СПОСОБ ВРАЩЕНИЯ

Сущность способа вращения также состоит в изменении положения объекта, заданного на комплексном чертеже (эпюре), таким образом, чтобы определенные его элементы заняли относительно плоскостей проекций частное положение и проецировались без искажения.

Вращение может производится вокруг осей, расположенных относительно плоскостей проекций различным образом.

Дата добавления: 2015-06-29