Показатели вариации. Средние величины, характеризуя вариационный ряд числом, не отражают изменчивости наблюдавшихся значений признака

Средние величины, характеризуя вариационный ряд числом, не отражают изменчивости наблюдавшихся значений признака, т.е. вариацию. Простейшим показателем вариации является вариационный размах (R_B), равный разности между наибольшим и наименьшим вариантами, т.е.

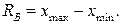(13)

Вариационный размах — приближённый показатель вариации, так как почти не зависит от изменения вариантов, а крайние варианты, которые используются для его вычисления, как правило, ненадёжны.

Более содержательными являются меры рассеяния наблюдений вокруг средних величин. Средняя арифметическая является основным видом средних, поэтому ограничимся рассмотрением мер рассеяния наблюдений вокруг средней арифметической.

Сумма отклонений результатов наблюдений 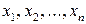от средней арифметической 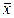, т.е. 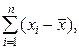не может характеризовать вариацию наблюдений около средней арифметической. В силу свойства1° эта сумма равна нулю. Берут или абсолютные величины, или квадраты разностей 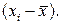В результате получают различные показатели вариации.

Средним линейным отклонением (d) называют среднюю арифметическую абсолютных величин отклонений результатов наблюдений от их средней арифметической:

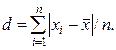(14)

Эмпирической дисперсией (s²) называют среднюю арифметическую квадратов отклонений результатов наблюдений от их средней арифметической:

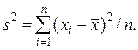(15)

Если по результатам наблюдений построен вариационный ряд, то эмпирическая дисперсия

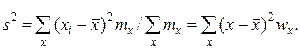(16)

Вместо эмпирической дисперсии в качестве меры рассеяния наблюдений вокруг средней арифметической часто используют эмпирическое среднеквадратическое отклонение, равное арифметическому значению корня квадратного из дисперсии и имеющее ту же размерность, что и значения признака.

Для вариационного ряда среднеквадратическое отклонение

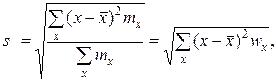(17)

где х — вариант (если ряд дискретный) и центр интервала (если ряд интервальный); m_x(w_x) — соответствующая частота (частость); 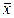— средняя арифметическая.

Для краткости величину s² часто будем называть просто дисперсией, не употребляя термина «эмпирическая». Однако при этом всегда следует помнить, что в этом случае дисперсия вычислена по результатам наблюдений на основании опытных данных, т.е. является эмпирической. Аналогичное замечание относится и к величине s.

Приведем свойство минимальности эмпирической дисперсии: s² меньше взвешенной средней арифметической квадратов отклонений вариантов от любой постоянной величины, отличной от средней арифметической, т.е.

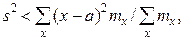
если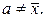

Доказательство. Найдём экстремум функции f(a)= 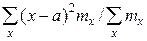. Для этого решим уравнение f'(a) =0. Имеем:

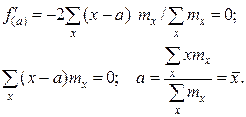
Так как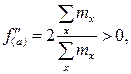то функция f(a) имеет в точке а= 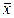минимум.

Можно показать, что среднее линейное отклонение не обладает свойством минимальности. Поэтому наиболее употребительными мерами рассеяния наблюдений вокруг средней арифметической являются эмпирическая дисперсия и эмпирическое среднеквадратическое отклонение.

Итальянский статистик Коррадо Джинни предложил в качестве показателя вариации использовать величину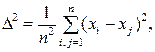

где 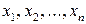- ряд наблюдений. Особенность этого показателя состоит в том, что он зависит только от разностей между наблюдениями и измеряет как бы «внутреннюю изменчивость» значений признака, а не их рассеяние вокруг какой-либо точки. Можно показать, что 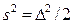, т. е. s ², являясь мерой рассеяния значений признака вокруг средней арифметической, характеризует также и внутреннюю их изменчивость.

Дата добавления: 2014-01-03