Доверительные вероятности, доверительные интервалы

Текст лекции

Лекция 17 Доверительные вероятности, доверительные интервалы

Учебные и воспитательные цели:

1. Дать представление о доверительных вероятностях и доверительных интервалах.

Вид занятия: лекция.

Продолжительность занятия: 90 минут.

Учебно-материальное обеспечение занятия:

Медиа-проектор, ноутбук, слайды Power Point (Оверхэд-проектор, слайды).

Литература:

а) основная:

1. Иванова В.М., Калинина В.Н., Нешумова Л.А., Решетникова И.О. Математическая статистика. 2-е изд., перераб. и доп. – М.: Высш. школа, 1981. – 371 с., ил.

Структура занятия и расчёт времени

Структура занятия	Время, мин
I. Вводная часть занятия
II. Основная часть занятия
Введение в лекцию
1. Доверительные вероятности, доверительные интервалы
Заключение по лекции
III. Заключительная часть занятия

Введение в лекцию:

В материалах сегодняшней лекции мы рассмотрим доверительные вероятности и доверительные интервалы.

Учебные вопросы лекции:

При статистической обработке результатов наблюдений необходимо знать не только точечную оценку 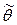параметра θ, но и уметь оценить точность этой оценки. Для этого введём понятие доверительного интервала.

Доверительным интервалом для параметра θ называется интервал содержащий значение θ с заданной вероятностью β.

Число β называется доверительной вероятностью.

Пусть 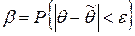- заданное число (оно обычно равно 0,8, 0,9, 0,95,...).

Так как 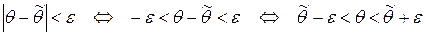, то интервал 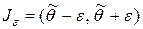содержит (накрывает) значение θ (рис. 1).

Интервал 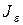- это доверительный интервал для параметра θ.

Покажем, как найти доверительный интервал для математического ожидания т_х с заданной доверительной вероятностью β.

Пусть 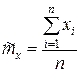- точечная оценка математического ожидания.

Используя центральную предельную теорему, можно считать, что слу­чайная величина

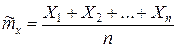
для больших п распределена по нормальному закону, а значит вероятности можно считать, используя функцию Лапласа Ф(х).

Тогда

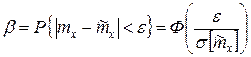
Отсюда .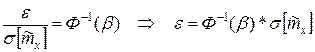

Здесь 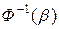находится по таблице Лапласа в обратном порядке: по

значению β функции Ф(х) находится аргумент 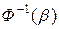, а .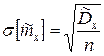

Таким образом, доверительный интервал для математического ожидании имеет вид

.

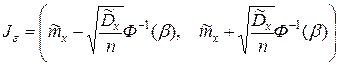Заключение по лекции:

В лекции мы рассмотрели доверительные вероятности и доверительные интервалы. В ходе подготовки к последующей лекции и практическим занятиям вы должны самостоятельно при углубленном изучении рекомендованной литературы и решения предложенных задач дополнить свои конспекты лекций.

Задание на самостоятельную работу

Изучить:

1. Иванова В.М., Калинина В.Н., Нешумова Л.А., Решетникова И.О. Математическая статистика. 2-е изд., перераб. и доп. – М.: Высш. школа, 1981. – 371 с., ил. стр 167-174.

Дата добавления: 2014-01-03