
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Эмпирические центральные и начальные моменты
Средняя арифметическая и дисперсия вариационного ряда являются частными случаями более общего понятия о моментах вариационного ряда.
Эмпирическим начальным моментом ( 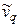 ) порядка q называют взвешенную среднюю арифметическую q-x степеней вариантов, т.е.
) порядка q называют взвешенную среднюю арифметическую q-x степеней вариантов, т.е.
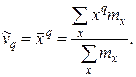 (20)
(20)
Эмпирический начальный момент нулевого порядка
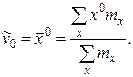
Эмпирический начальный момент первого порядка 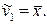
Эмпирический начальный момент второго порядка 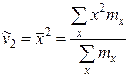 и т.д.
и т.д.
Эмпирическим центральным моментом (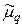 ) порядка q называют взвешенную среднюю арифметическую q-x степеней отклонений вариантов от их средней арифметической, т.е.
) порядка q называют взвешенную среднюю арифметическую q-x степеней отклонений вариантов от их средней арифметической, т.е.
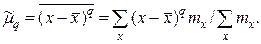 (21)
(21)
Эмпирический центральный момент нулевого порядка
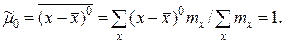 Эмпирический центральный момент первого порядка
Эмпирический центральный момент первого порядка 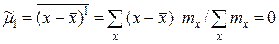
(в силу свойства 1° средней арифметической).
Эмпирический центральный момент второго порядка
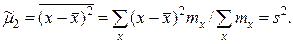
В дальнейшем для краткости величину 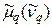 часто будем называть просто центральным моментом (начальным моментом), не употребляя термин «эмпирический».
часто будем называть просто центральным моментом (начальным моментом), не употребляя термин «эмпирический».
Используя формулу бинома Ньютона, разложим в ряд выражение для центрального момента q- го порядка:
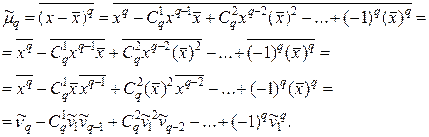
В проведенных тождественных преобразованиях использованы свойства 5° и 3° средней арифметической; 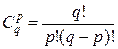 — число сочетаний из q элементов по р элементов (p≤.q).
— число сочетаний из q элементов по р элементов (p≤.q).
Итак, центральный момент q- го порядка выражается через начальные моменты следующим образом:
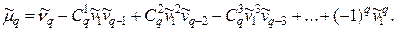 (22)
(22)
Полагая q = 0, 1, 2,…, можно получить выражения центральных моментов различных порядков через начальные моменты:
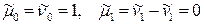 ;
;
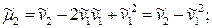 (23)
(23)
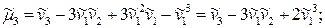 (24)
(24)
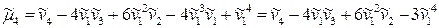 (25)
(25)
и т.д.
Заметим, что формула (23) для центрального момента второго порядка, как и следовало ожидать, аналогична формуле (18) для дисперсии.
Рассмотрим свойства центральных моментов, которые позволят значительно упростить их вычисление.
1°. Если все варианты уменьшить (увеличить) на одно и то же число с, то центральный момент q-го порядка не изменится.
Доказательство. Если все варианты уменьшить на число с, то средняя арифметическая для измененного ряда равна 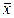 - с, поэтому центральный момент q- го порядка
- с, поэтому центральный момент q- го порядка
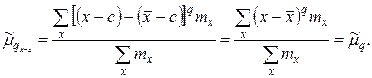
Аналогично можно показать, что 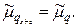
2°. Если все варианты уменьшить (увеличить) в одно и то же число k раз, то центральный момент q-го порядка уменьшится (увеличится) в 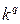 раз.
раз.
Доказательство. Если все варианты уменьшить в одно и то же число k раз, то средняя арифметическая для измененного вариационного ряда равна 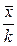 , поэтому центральный момент q-гo порядка
, поэтому центральный момент q-гo порядка
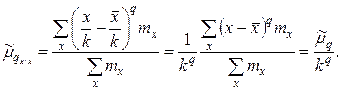
Аналогично можно показать, что 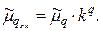
Для облегчения расчётов центральные моменты вычисляют не по первоначальным вариантам х, а по вариантам х'=(х — с)/k. Зная 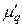 (центральный момент q- го порядка для измененного ряда), легко вычислить центральный момент q -го порядка для первоначального ряда:
(центральный момент q- го порядка для измененного ряда), легко вычислить центральный момент q -го порядка для первоначального ряда:
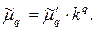 (26)
(26)
Действительно, принимая во внимание свойства центрального момента, получаем
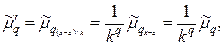
откуда следует, что 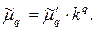
|
|
Дата добавления: 2014-01-03; Просмотров: 1561; Нарушение авторских прав?; Мы поможем в написании вашей работы!