Приклади розв’язування задач. При поширенні в пружному середовищі декількох хвиль коливання кожної частинки середовища згідно з принципом суперпозиції уявляє суму коливань від кожної

Стоячі хвилі.

При поширенні в пружному середовищі декількох хвиль коливання кожної частинки середовища згідно з принципом суперпозиції уявляє суму коливань від кожної хвилі. В загальному випадку це коливання буде нагадувати биття коливань. Картина поширення хвиле не буде стаціонарною, тобто в кожний момент часу амплітуда і частота коливань деякої точки середовища будуть змінюватись.

Якщо ж різниця фаз двох хвиль не змінюється з часом, такі хвилі називаються когерентними, і картина складання коливань буде стаціонарною. В одних точках спостерігається підсилення коливань, в інших послаблення. Це явище називається інтерференцією.

Одним із прикладів інтерференції є накладання двох когерентних зустрічних хвиль, які утворюються при відбиванні біжучої хвилі від перешкоди. Так утворюється стояча хвиля.

Знайдемо її рівняння. Нехай рівняння прямої біжучої хвилі має вид 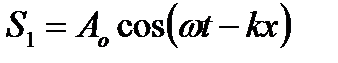. Тоді рівняння відбитої хвилі буде таким . Результуючим буде коливання

.

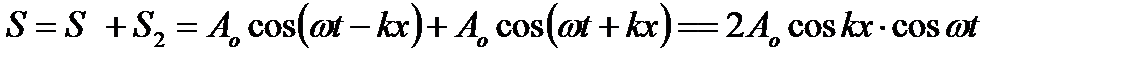
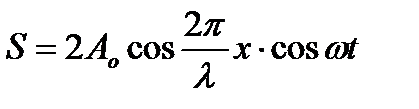Видно, що кожна точка середовища з координатою х здійснює гармонічне коливання з циклічною частотою ω і амплітудою, яка залежить від координати х

.

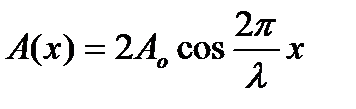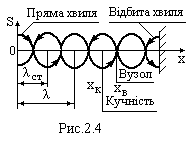
Точки, в яких амплітуда максимальна, називаються кучностями, а в яких дорівнює нулю – вузлами (рис. 6).

Координати кучностей х_к знаходяться із умови _, а вузлів із умови . Одержимо

, .

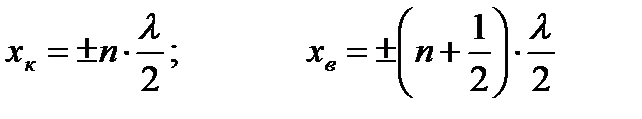Довжина стоячої хвилі – це відстань між сусідніми вузлами або кучностями. Вона в два рази менша, ніж довжина біжучої хвилі . Стояча хвиля не переносить енергію, а відбувається перетворення кінетичної енергії у пучності в потенціальну енергію деформації у вузлі.

Запитання до самоперевірки.

1 Що називають гармонічним осцилятором?

2 Дати визначення й записати формулу математичного маятника.

3 Що називають фізичним маятником?

4 Розкрити суть енергії коливального руху.

5 Як знайти результуючий рух точки, що одночасно перебуває у двох гармонічних коливаннях однакової частоти?

6 Як поділяються хвилі залежно від напряму коливань точок відносно променя?

7 Пояснити механізм утворення стоячих хвиль.

Задача 1. Частинка здійснює гармонічні коливання вздовж осі х біля положення рівноваги х = 0. Циклічна частота коливань w = 4 c^-1. В момент часу t = 0 координати частинки х₀ = 25,0 см, а її швидкість υ = 100 см/с. Знайти координату х і швидкість υ цієї частинки через t = 2,40 с.

Дано:

w = 4 с^-1

х₀ = 25,0 см

υ= 100,0 см/с

t = 2,40 с

___________

х –? υ –?

Розв’язування. Рівняння гармонічних коливань має вигляд:

x = A cos (w t + j). (1)

Швидкість частинки в довільний момент часу дорівнює:

υ = - A w sin (w t + j). (2)

В початковий момент часу t = 0 величини х і υ відповідно дорівнюють х₀ і υ₀:

x₀ = A cos j i υ₀ = - Aw sin j. (3)

Розв’язавши систему рівнянь (3), одержимо значення амплітуди коливань і початкової фази:

= 1 звідки А = ;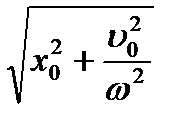

cos j = звідки j = arc cos .

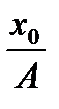Числові значення амплітуди і початкової фази в одиницях умови задачі

A = 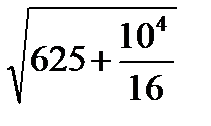= 35,5 cм, j = arc cos .

Скориставшись значеннями амплітуди коливань і початкової фази, знаходимо координату х і швидкість υ в момент часу t:

x = 35,5 cos (4 × 2,40 + p/4) = - 20,2 см, υ = - 35,5 × 4sin (4 × 2,40 + p/4) = 115,7 см/с.

Відповідь: х = - 20,2 см; υ = 115,7 см/с.

Задача 2. В результаті додавання двох гармонічних коливань однакового напрямку і близьких частот одержали результуюче рівняння x = A cos 2,1 t cos 50,0 t см. Визначити циклічні частоти коливань, які додаються, і період биття.

Дано:

x = A cos 2,1 t cos 50,0 t см

_______________________

w₁ –? w₂ –? Т_б –?

Розв’язування. Відомо, що при додаванні двох гармонічних коливань з близькими частотами w₁ і w₂ рівняння результуючого руху має вигляд:

х = .

Порівнюючи це рівняння і рівняння умови задачі, маємо

= 2,1 c^-1 i 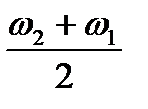= 50,0 c^-1

Звідки w₁ = 47,9 c^-1; w₂ = 52,1 c^-1.

Періодичність зміни амплітуди визначається періодичністю зміни модуля косинуса:

T_б = , де Т_б – період биття.

Знаходимо період биття T_б = 1,49 с

Відповідь: w₁ = 47,9 с^-1; w₂ = 52,1 с^-1; Т_б = 1,49 с.

Задача 3. Задаються рівняння руху частинки х = Аsin wt і y = В cos wt, де А і В – амплітуди коливань частинки вздовж координатних осей х і y. Знайти: а) рівняння траєкторії частинки у(х) і напрям її руху вздовж цієї траєкторії; б) прискорення а в залежності від напряму радіуса вектора .

Дано:

х = Аsin wt

y = В cos wt

___________

у(х) –? а –?

Розв’язування. Рівняння траєкторії частинки одержимо, якщо рівняння (1) і (2) записати в такому вигляді:

sin wt = 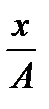, cos wt = . Піднесемо до квадрата:

= sin²wt; = cos² wt;

Додавши ці рівняння одержимо: + 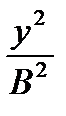= 1 – еліпс.

Будуємо цю траєкторію в декартовій системі координат (рис.1):

Рисунок 1

Аналізуючи рівняння умови задачі в різні моменти часу, знаходимо, напрям руху частинки вздовж траєкторії:

а) при t = 0, х = 0 і у = В – початок руху;

б) при t = p/4, х = А і у = 0 – наступна точка;

в) при t = T/2, х = 0 і у = -В і т. д.

Результуюче прискорення руху частинки визначаємо із відповідних прискорень руху вздовж осей х і у:

υ_х = А wсos wt; а_х= - А w² sin wt = - w² x;

υ_y = - В w sin wt; a_y= - Вw² cos wt = - w² y;

Модуль вектора 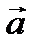дорівнює

a = w² 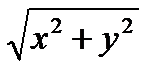= w² r.

Радіус-вектор частинки завжди направлений від початку координат до положення точки на траєкторії. Вектор результуючого прискорення завжди направлений від положення частинки на траєкторії руху до початку координат, тобто

a = - w² r.

Задача 4. Однорідний стрижень поклали на два блоки, які швидко обертаються, як це показано на рис.2. Відстань між осями блоків l = 20 см, коефіцієнт тертя ковзання між стрижнем і блоками k = 0,18. Показати, що стрижень буде здійснювати гармонічні коливання. Знайти період цих коливань.

Дано: l = 20 см k = 0,18 ________ Т –?

Рисунок 2

Розв’язування. При зміщенні стрижня вліво на величину х від положення рівноваги сили тертя F₁ i F₂, які виникають між стержнем і блоками дорівнюють

F₁ = 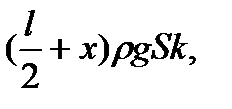F₂ =

де r – густина матеріалу стрижня;

S – переріз стрижня;

k – коефіцієнт тертя ковзання.

Повертаюча сила, яка виникне в цьому випадку, буде дорівнювати:

F = – (F₁ -F₂) = - 2 r g S k x. (1)

За другим законом Ньютона ця ж сила дорівнює:

F = m a. (2)

Порівнюючи праві частини рівностей (1) і (2), маємо

ma + 2 r g S k x = 0

aбо

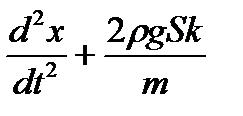x = 0. (3)

Одержане диференціальне рівняння (3) є рівнянням гармонічних коливань. Циклічна частота цих коливань визначається співвідношенням:

w² =

звідки

T = 2p

або врахувавши, що m = rlS, одержимо: T = 2p .

Підставимо числові значення:

T = 1,5 с.

Відповідь: Т = 1,5 с.

Задача 5. Фізичний маятник у вигляді тонкого прямого стрижня довжиною 120 см коливається біля горизонтальної oсі, яка проходить перпендикулярно до стрижня через точку, віддалену на деяку відстань а від центра мас стрижня. При якому значенні а _е період коливань буде мати найменше значення? Знайти величину цього періоду?

Дано:

l = 120 см

_________

а_e –?

Т_min –?

Розв’язування. Відведений від положення рівноваги стрижень буде здійснювати коливання відносно закріпленої осі, яка збігається з віссю Z (рис.3). Покажемо, що при малих кутах відхилення (j < 7°), ці коливання будуть гармонічними. В будь-який момент часу на стрижень діють дві сили, сила тяжіння і сила реакції опори. Однак, обертаючий момент створюється лише силою тяжіння.

M =- mga sin j, (1)

де а – відстань від осі обертання до центра мас стрижня;

j – кут відхилення стрижня від положення рівноваги.

Для малих кутів sinj = j, а напрям вектора 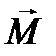протилежний до напрямку осі Z, тому

M_z = - mga j, (2)

Згідно з основним рівнянням динаміки обертального руху цей момент дорівнює:

M_z = І 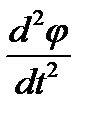. (3)

Прирівняємо праві частини рівностей (2) і (3), одержимо:

I 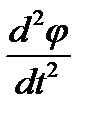+ mga j = 0.

Звідки: 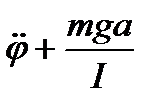j = 0. (4)

Рівняння (4) є диференціальним рівнянням гармонічних коливань, квадрат циклічної частоти яких дорівнює:

(5)

де І – момент інерції стрижня відносно осі обертання;

а – відстань від точки підвісу до центра мас.

Момент інерції стрижня знайдемо за теоремою Штейнера згідно з якою:

I = I₀ + m a²,

де І₀ = ml² – момент інерції стрижня відносно осі, яка проходить через центр мас стрижня. Тому

І = 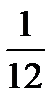m l² + ma². (6)

Підставимо (6) в (5) і визначимо період коливань

T = 2p . (7)

Для визначення екстремальної відстані а_е від центра мас до точки підвісу, похідну за а підкореневого виразу формули (7) прирівняємо до нуля:

= 0, .

Звідки

2 a ² - 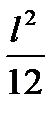- a ² = 0;

a _e = ± . (8)

a_e = ± 0,34 м.

Величину а _е з (8) підставимо в (7) і знайдемо значення найменшого періоду коливань фізичного маятника:

T_min = 2p = 1,67 c.

Відповідь: а_е = 34 см; Т_min = 1,67 c.

Задача 6 Труба має довжину 85 см. Вважаючи швидкість звуку 340 м/с, визначити число власних коливань стовпа повітря в трубі, частоти яких менше n₀ = 1250 Гц. Розглянути два випадки: а) труба закрита з одного кінця; б) труба відкрита з обох кінців.

Дано:

l = 0,85 м

υ = 340 м/с

n₀ = 1250 Гц

____________

n₁ –? n₂ –?...

Розв’язування. В трубі як в першому, так і в другому випадку створюється стояча хвиля. Слід мати на увазі, що біля відкритого кінця труби завжди буде пучність, а біля закритого кінця труби завжди буде вузол, як це показано на рис.

а) у випадку закритої з одного кінця труби на її довжині вкладається непарне число l/4, тобто l = (2k +1) l/4, де k = 0, 1, 2,...;

l – довжина хвилі, яка пов’язана з частотою коливань l = υ/n.

Тому

l = (2k + 1) , звідки n = .

Знайдемо ці частоти

k = 0; n₁ = = 100 Гц.

k = 1; n₂ = = 300 Гц.

k = 2; n₃ = = 500 Гц.

k = 3; n₄ = = 700 Гц.

k = 4; n₅ = 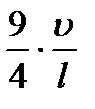= 900 Гц.

k = 5; n₆ = = 1100 Гц.

Наступна частота буде більша за n₆;

б) у випадку відкритої з обох кінців труби, для збереження умови пучностей біля відкритого кінця, треба, щоб в її довжині вкладалось ціле число півхвиль, тобто

l = k 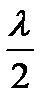, де k = 1, 2, 3,.З урахуванням того, що l = , маємо

l = k , звідки n = .

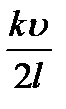Знайдемо ці частоти

k = 1; n₁ = = 200 Гц. k = 2; n₂ = = 400 Гц.

k = 3; n₃ = = 600 Гц. k = 4; n₄ = 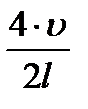= 800 Гц.

k = 5; n₅ = = 1000 Гц. k = 6; n₆ = = 1200 Гц.

Задача 7 На шосе рухаються назустріч дві автомашини з швидкостями u₁ = 30 м/c і u₂ = 20 м/с. Перша з них подає звуковий сигнал частотою n₁ = 600 Гц. Визначити частоту, яка буде сприйматись водієм другої автомашини в двох випадках: а) до зустрічі; б) після зустрічі. Швидкість звуку в повітрі c = 340 м/с.

Дано:

u₁ = 30 м/с

u₂ = 20 м/с

n₀ = 600 Гц

c = 340 м/с

____________

–? –?

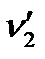Розв’язування. Зміна частоти коливань при русі джерела звуку і приймача в цих випадках визначається за допомогою формули ефекту Допплера:

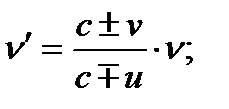
а) до зустрічі

× 600 = 696 Гц;

б) після зустрічі

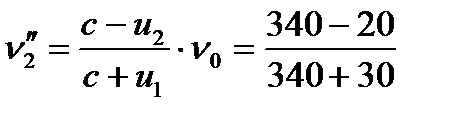× 600 = 519 Гц.

Відповідь: = 696 Гц; = 519 Гц.

Задача 8 Визначити потужність точкового ізотропного джерела звуку, якщо на відстані r = 25 м від нього інтенсивність звуку R дорівнює 20 мВт/м². Яка середня густина енергії на цій відстані?

Дано:

r = 25 м

R = 20 мВт/м²

_____________

N –? –?

Розв’язування. Відомо, що інтенсивність або густина потоку енергії визначається за формулою

R = ,

де W – повна енергія, яка випромінюється точковим джерелом звуку у всіх напрямках;

S – площа поверхні, через яку здійснюється перенесення енергії;

Dt – час випромінювання.

Тоді потужність точкового джерела випромінювання буде дорівнювати

N = 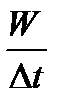або N = R S.

Підставимо числові значення

N = 20 × 10^-3 × 4 × 3,14 × 625 = 157 Вт.

Середня об’ємна густина енергії на цій відстані визначається з формули

R = 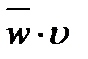звідки = ,

де – швидкість звуку в повітрі, яка для норальних умов дорівнює 340 м/с.

Тому

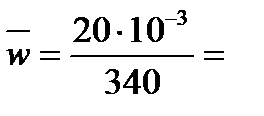5,88 × 10^-5 Дж/м³.

Відповідь: 157 Вт; 5,85×10^-5 Дж/м³.

Дата добавления: 2017-01-14