Графічне зображення електричного поля

Електричні поля зображають за допомогою ліній напруженості, які проводять так, щоб дотичні до цих ліній в кожній точці збігалися з напрямками вектора (рис.).

Лінії напруженості мають початок і кінець або йдуть у нескінченність чи з нескінченності, вони напрямлені від позитив­ного заряду до негативного, тобто виходять з позитивного заряду, а входять у негативний заряд. Лінії напруженості ніколи не перетинаються. Ці лінії проводять з такою густиною, щоб кількість ліній, які пронизують одиничну площу, перпендикулярну до вектора напруженості, числово дорівнювала величині напруженості електричного поля в місці розміщення площини. Приклади графічного зображення електричних полів за допомогою ліній напруженості показано на рис.

Поле, у всіх точках якого величина і напрямок вектора напруженості незмінні, називається однорідним.

Воно утворюється між зарядженими площинами, якщо вони паралельні і нескінченно великі. Однорідне поле зображують паралельними лініями напруженості, що мають однакову густину.

Якщо поле створено системою N нерухомих зарядів, то результуюча сила, яка діє на пробний заряд зі сторони системи зарядів, дорівнює векторній сумі сил, з якими окремі заряди діють на пробний.

Напруженість поля системи точкових зарядів дорівнює векторній сумі напруженостей полів, які створював би кожний із зарядів системи зокрема:

,

.

Це твердження називають принципом незалежності дії електричних полів, або принципом суперпозиції полів.

Розглянемо декілька прикладів застосування принципу суперпозиції для розрахунку поля заряджених тіл.

Приклад 1 Розрахувати напруженість електричного поля на осі зарядженого кільця радіусом R, зарядом q на відстані h від центра кільця (рис.).

Елемент dl₁ кільця, заряд якого 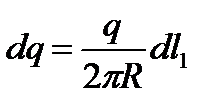, створює напруженість поля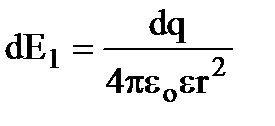

Діаметрально протилежний елемент dl₂ створює напруженість dE₂. Ясно, що Х–ві проекції цих векторів попарно компенсуються, а У-ві – додаються.

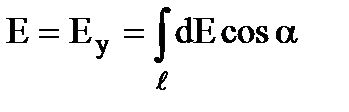. Враховуючи, що 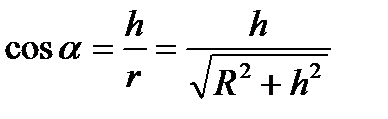, одержуємо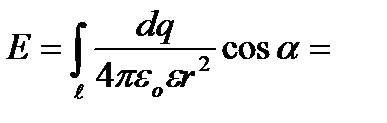

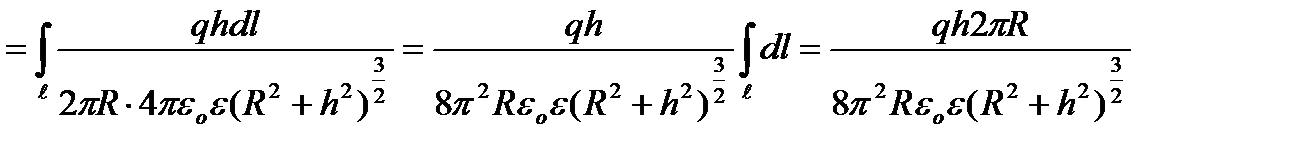
При h =0 (в центрі кільця) Е=0. При h → ∞ Е = 0.

Приклад 2 Розрахувати поле нескінченної зарядженої осі в точці, яка знаходиться на відстані R від неї. Лінійна густина заряду осі дорівнює τ (рис.).

Нескінченно малий елемент dℓ(точковий заряд) створює напруженіcть . Заряд цього елемента дорівнює 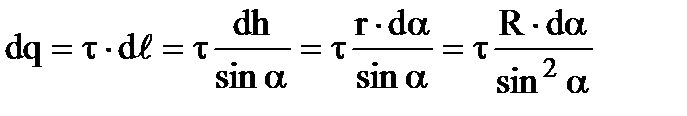. Відстань . Одержуємо . Знаходимо проекції цього вектора на осі координат: , 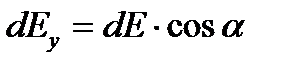. Інтегрування по всій осі зводиться до інтегрування по куту α в межах від 0 до π.

.

.

Так як Е_у = 0, вектор напруженості направлений вздовж осі ох, тобто перпендикулярно до зарядженої осі.

Приклад 3 Розрахувати поле нескінченної зарядженої площини з поверхневою густиною заряду σ.

Положення нескінченно малого елемента dS, заряд якого dq = σ∙dS,

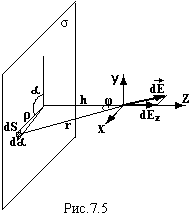задамо полярними координатами ρ і α. В цих координатах S = ρ∙dρ∙dα. Знайдемо dE_z, яка перпендикулярна до площини. Щоб охопити всю площину, кут α повинен змінюватись від 0 до 2π, а радіус ρ – від 0 до ∞. Беремо подвійний інтеграл в цих межах

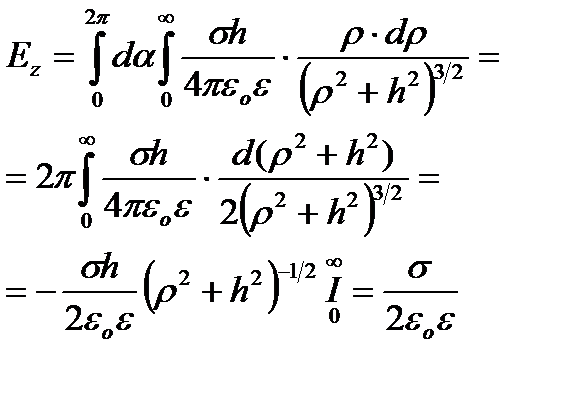
Проекція вектора напруженості на площину, перпендикулярну до осі ОZ дорівнює нулю. В цьому можна впевнитись математично, замінивши соsφ на sinφ, а можна і такими міркуваннями: на нескінченній площині завжди можна знайти елемент dS₂, симетричний dS₁ відносно перпендикуляра h до площини (рис). Ці елементи створюють однакові вектори напруженості dE₁ і dE₂, Z-ві проекції яких співпадають, а перпендикулярні проекції взаємно протилежні і тому компенсують одна одну. Отже вектор напруженості поля нескінченної зарядженої площини

перпендикулярний до неї і не залежить від положення точки, тобто однакове в усіх точках простору. Такі поля називаються однорідними.

Для спрощення розрахунку полів симетричних заряджених тіл застосовується теорема Остроградського – Гауса: потік вектора електростатичної індукції через будь-яку замкнуту поверхню дорівнює алгебраїчній сумі зарядів, охоплених цією поверхнею. .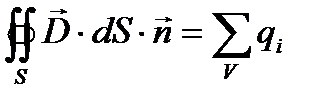

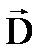Потоком dФ вектора через площадку dS називається добуток вектора на величину площадки dS і на косинус кута α між вектором 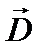і нормальним до площадки dS одиничним вектором .

.

Приклади розв’язування задач

Задача 1 Протон і електрон атому водню зазнають гравітаційне і електричне притягання. Яка із взаємодій більша і в скільки разів?

Дано:

m_e=9,1·10^-31кг m_p=1,67·10^-27кг =1,6·10¹⁹ Кл q_p=1,6·10^-19Кл G=6,67·10^-11 (H·м²)/кг² к=9·10⁹ Н·м²/Кл²

Розв’язування

Відповідь: 25∙10³⁸.

Задача 2 Заряди 40 нКл і –10 нКл розташували на відстані 10 см один від одного. Яким треба взяти третій заряд щоб система перебувала у рівновазі? Де треба його розташувати?

Дано:

q₁=40·10^-9Кл q₂=-10·10^-9Кл R=10·10^-2м

R₁-? R₂-? q₃-?

Розв’язування

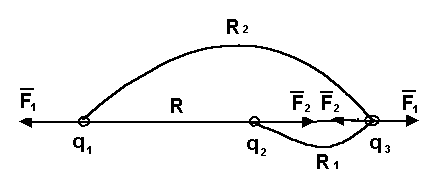
Якщо заряди q₁ і q₂ різнойменні, то заряд q₃ розташовують на прямій за тим зарядом, який менший за модулем.

,

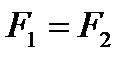
; R₂=R+R₁

; ;

;

;

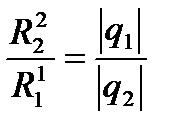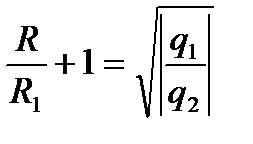
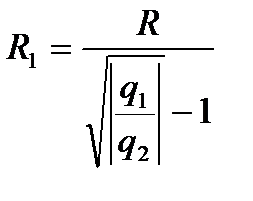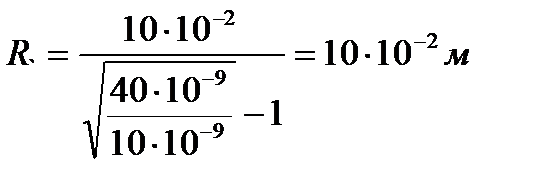
R₁=10 см, R₂=20 см

Відповідь: на відстані 10 см від меншого за модулем заряду і на відстані 20 см від більшого.

Задача 3 Однакові металеві кульки q₁=5 нКл і q₂=11 нКл знаходяться на відстані 8 мм одна від одної. Кульки доторкнули одну до одної. На яку відстань їх треба розвести, щоб сила взаємодії не змінилася?

Дано:

q₁=5·10^-5 Кл q₂=11·10^-9Кл R₁=8·10^-3м F₁=F₂

R₂-?

Розв’язування

,

,

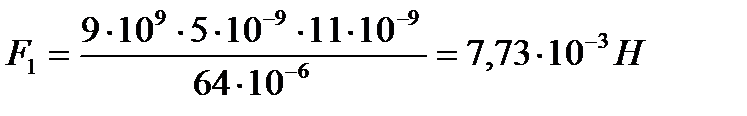
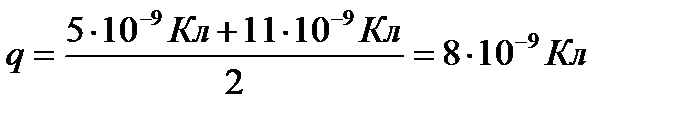
Відповідь: 8,63 мм.

Задача 4 Дві однакові металеві кульки зарядили так, що заряд однієї з них у 10 разів більший, ніж другої. Кульки доторкнули одну до одної і розвели на попередню відстань. У скільки разів (за модулем) зміниться сила їхньої взаємодії 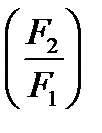, якщо: 1) заряди однойменні; 2) різнойменні.

Дано:

q₁=q q₂=10q R₁=R₂=R

Розв’язування

1)

,

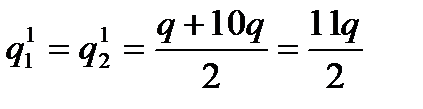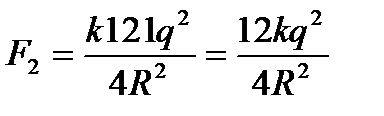
2) , ,

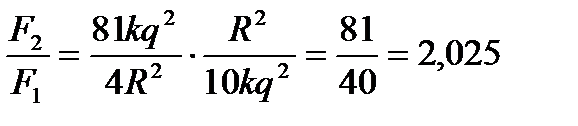
Відповідь: 3,025, 2,025.

Задача 5 Дві однакові металеві кульки масою по 0,25 г підвішено в одній точці на нитках довжиною 30 см. Після надання їм від’ємного заряду кульки розійшлися на відстань 20 см одна від одної. Скільки електронів було передано кулькам?

Дано:

m₁=m₂=m= 0,25г=0,25·10^-3 кг l=30см=0,3м d=20см=0,2м q₁=q₂=q

N-?

Розв’язування

OX: Ncosα-mg=0,

OY: F_ел-Nsinα=0

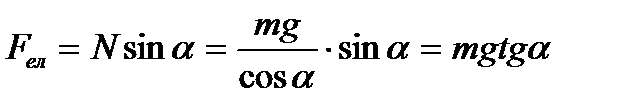
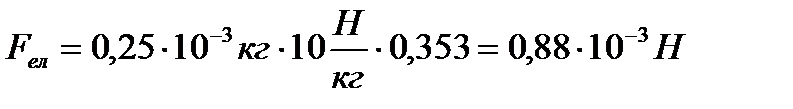
Відповідь: 6,25∙10^-8.

Задача 6 Дві однакові металеві заряджені кульки знаходяться на відстані 10 см одна від одної. Сила відштовхування кульок 50 мкН. Після дотику та віддалення кульок на початкову відстань сила відштовхування стала рівною 120 мкН. Знайдіть заряди кульок перед дотиком.

Дано:

R=0,1 м F₁=50·10^-6H F₂=120·10^-6H

q₁-? q₂-?

Розв’язування
Після дотику:

,

;

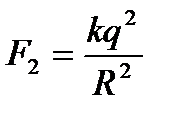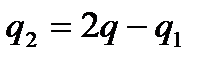
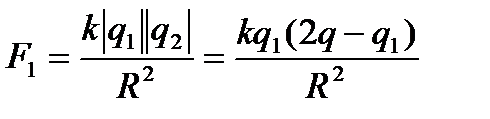
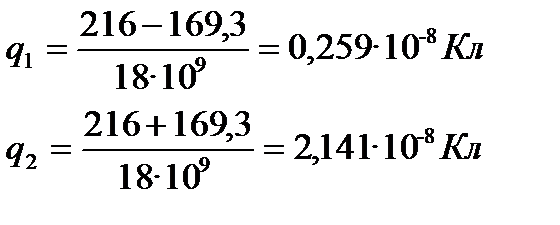
Відповідь: 0,259∙10^-8Кл, 2,141∙10^-8Кл.

Задача 7 Визначити напруженість поля в точках С і Д, якщо два заряди q₁=30 нКл і q₂=-20 нКл знаходиться в точках А і В, а відстані дорівнюють: АС=5 см, СВ=4 см, ВД=3 см.

Дано:

q₁=30·10^-9Кл q₂=-20·10^-9Кл АС=5·10^-2м СВ=4·10^-2м ВД=3·10^-2м

Е_с-? Е_д-?

Розв’язування

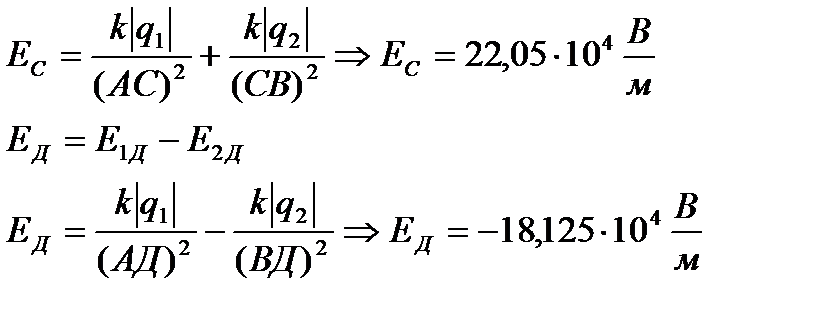
Відповідь: 22,05∙10⁴ В/м, - 18,125∙10⁴ В/м.

Задача 8 У двох вершинах А і С квадрату із стороною а=3 см розташовані різнойменні заряди q₁ і q₂, модулі яких однакові і дорівнюють 2·10^-6 Кл. Знайдіть напруженість поля у двох інших вершинах квадрату.

Дано:

a=3 м q₁=2·10^-6Кл q₂=-2·10^-6Кл

E_B-? E_Д-?

Розв’язування

,

Відповідь: 3∙10³ Н/Кл, 3∙10³ Н/Кл.

Задача 9 Заряди по 0,1 мкКл розташували на відстані 6 см один від одного. Визначити напруженість поля в точці, віддаленій на 5 см від кожного із зарядів.

Дано:

q₁=q₂=q=0,1·10^-6 Кл R₁=6 см = 6·10^-2м R₂=5 см= 5·10^-2м

E-?

Розв’язування

, ,

, ,

.

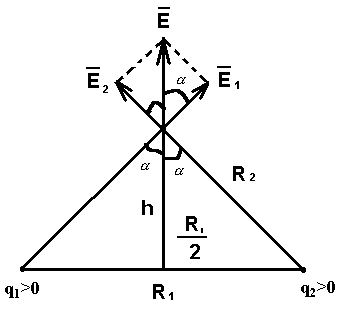
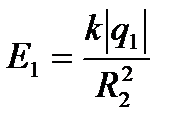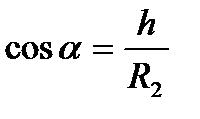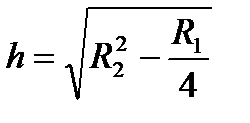
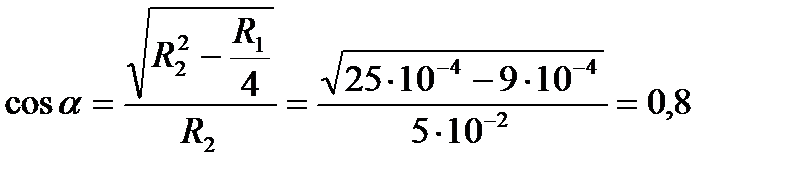
Відповідь: 576∙10⁶ В/м.

Задача 10 У трьох вершинах квадрата, сторона якого становить 0,4 м, розташували однакові позитивні заряди по 0,5·10^-9 Кл. Визначити напруженість поля в четвертій вершині.

Дано:

а=0,4 м q₁=q₂=q₃=q= =5·10^-9Кл

E_Д-?

Розв’язування

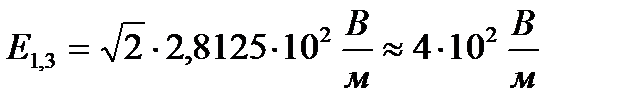
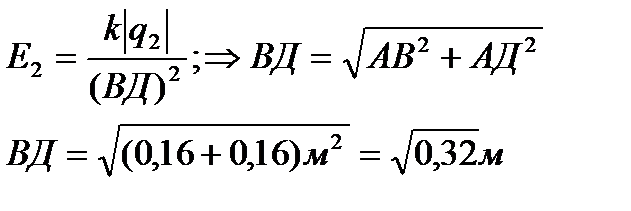
Відповідь: 540 В/м.

Задача 11 На тонкому стержні, довжина якого l, рівномірно розподілений заряд з лінійною густиною t=10 нКл/м. Знайти потенціал j, створений розподіленим зарядом в точці А, яка розміщена на осі стержня і віддалена від ближчого кінця на відстань l.

t=10 нКл/м

_________

j-?

Розв’язок.

Виділимо на стержні малий елемент довжиною dx, заряд якого 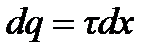можна вважати точковим. Потенціал j в точці А можна визначити за формулою:

Згідно з принципом суперпозицій електричних полів, потенціал електричного поля, створеного зарядженим стержнем в точці А, знайдемо інтегруванням цього виразу:

Підставимо числові значення:

Відповідь. j=62,4 В.

Дата добавления: 2017-01-14