
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Задачі для самостійного виконання
|
|
|
|
Розв’язання.
Коло
Приклади.
Криві другого порядку
Відповіді: 2. 3. 4. 5. 6. 7. 8. 9. 10..
Рівняння вигляду

де хоча б один з коефіцієнтів  або
або  відмінний від нуля, називається алгебраїчним рівнянням першого порядку, або першого степеня відносно змінних
відмінний від нуля, називається алгебраїчним рівнянням першого порядку, або першого степеня відносно змінних 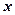 і
і  .
.
Рівняння (35) завжди описує пряму лінію.
Алгебраїчним рівнянням другого порядку називається всяке рівняння вигляду

де хоча б один з коефіцієнтів 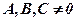 .
.
Лінії, координати точок яких задовольняють рівняння (36) називаються лініями другого порядку. До ліній другого порядку відносяться: еліпс (зокрема коло), гіпербола, парабола. Вони описуються рівнянням вигляду (36). Однак не кожне рівняння другого порядку завжди описує одну із згаданих ліній. Може, наприклад, вийти так, що рівняння вигляду (36) описує пару прямих ліній або не визначає жодного реального об’єкту.
1. Рівняння 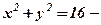 описує коло.
описує коло.
2. Рівняння  описує параболу.
описує параболу.
3. Рівняння  розпадається на дві прямі
розпадається на дві прямі 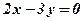 і
і  , що перетинаються.
, що перетинаються.
4. Рівняння  , тобто
, тобто  розпадаються на дві паралельні прямі
розпадаються на дві паралельні прямі  і
і 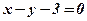 .
.
5. Рівняння  , тобто
, тобто 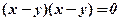 розпадається на дві прямі, що збігаються.
розпадається на дві прямі, що збігаються.
6. Рівняння  має своїм розв’язком тільки одну точку
має своїм розв’язком тільки одну точку 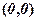 .
.
7. Рівняння 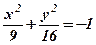 не описує в області дійсних чисел ніякого геометричного місця точок.
не описує в області дійсних чисел ніякого геометричного місця точок.
Додамо ще, що при відповідному виборі декартової системи
координат рівняння (36) для кривих другого порядку набувають простий, так званий канонічний вигляд. Далі розглянемо коротко кожну із кривих другого порядку.
Означення. Колом називається множина точок  площини, які знаходяться на відстані R від заданої точки
площини, які знаходяться на відстані R від заданої точки 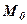 .
.
Нехай  – центр кола,
– центр кола,  – довільна точка кола. За умовою
– довільна точка кола. За умовою  , а за формулою відстані між двома точками маємо
, а за формулою відстані між двома точками маємо

– рівняння кола радіуса  з центром в точці
з центром в точці  .
.
Якщо ж центр кола збігається з початком координат, 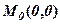 , то отримуємо
, то отримуємо

-канонічне рівняння кола.
Розкриємо дужки в (37) і зведемо його до вигляду (36)
 .
.
Отже загальне рівняння (36) може описувати коло, якщо  а
а  . За цих умов, щоб знайти центр кола і його радіус, потрібно виділити повний квадрат.
. За цих умов, щоб знайти центр кола і його радіус, потрібно виділити повний квадрат.
Приклад. Знайти центр кола і радіус, якщо
1. 
Розв’язання. Згрупуємо відносно 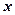 і
і  , а тоді виділимо повні квадрати
, а тоді виділимо повні квадрати
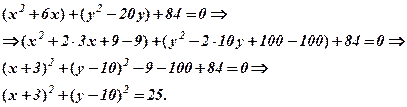
Отже, центр кола в точці 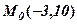 , а радіус
, а радіус  . Пропонуємо побудувати це коло.
. Пропонуємо побудувати це коло.
2. 

Сумма квадратів в лівій частині рівності не може бути від’ємною.
Дане рівняння не описує кола.
1. За рівняннями а)  , б)
, б)  , в)
, в)  знайти центри та радіуси кіл.
знайти центри та радіуси кіл.
2. Скласти рівняння кола з центром у точці С і радіусом R: 1) С(-6,-3), R=5; 2) C(1,-2),  ; 3) C(2,0), R=3; 4) C(0,-1), R=1,5.
; 3) C(2,0), R=3; 4) C(0,-1), R=1,5.
3. Для поданих рівнянь кіл знайти координати їх центрів і радіуси: 1)  ;
;
2)  ; 3)
; 3)  .
.
4. Скласти рівняння кола, якщо кінці його діаметра містяться у точках А(-3,-1) і В(1,5).
5. Скласти рівняння кола з центром в точці О(0,0), яке дотикається прямої  .
.
6. Записати рівняння кола з радіусом рівним 13, яке проходить через точки А(3,-1), і В(-4,-8).
7. Трикутник заданий вершинами L(-3,6), M(-1,10), N(6,9). Записати рівняння описаного навколо DLMN кола.
8. Написати рівняння дотичної до кола  в точці М(5,3).
в точці М(5,3).
9. Коло задане рівнянням  . Скласти рівняння дотичної до кола в точці М(0,1).
. Скласти рівняння дотичної до кола в точці М(0,1).
10. Знайти відстань між центрами кіл  і
і 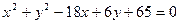 .
.
Відповіді: 1. а) С(-4,2), R=6; б) С(0,-3),  ; в) С(4,-2),
; в) С(4,-2), 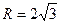 . 2. 1)
. 2. 1) 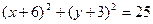 ; 2)
; 2)  ; 3)
; 3)  ;
;
4)  .
.
3. 1)  ; 2)
; 2)  ; 3)
; 3)  . 4.
. 4.  .
.
5. 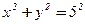 .
.
6.  або
або 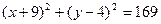 .
.
7.  . 8.
. 8. 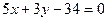 .
.
9. 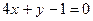 . 10. 10.
. 10. 10.
|
|
|
|
|
Дата добавления: 2017-01-14; Просмотров: 224; Нарушение авторских прав?; Мы поможем в написании вашей работы!