
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Задачі для самостійного розв’язання. Означення. Параболою називається множина точок площини, які рівновіддалені від заданої точки, що називається фокусом і заданої прямої
|
|
|
|
Парабола
9.112. 10..
Означення. Параболою називається множина точок площини, які рівновіддалені від заданої точки, що називається фокусом і заданої прямої, що називається директрисою.
Для отримання канонічного рівняння параболи розмістимо директрису перпендикулярно осі  , а фокус
, а фокус 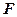 на осі
на осі  так, щоб початок координат
так, щоб початок координат 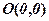 містився на однаковій відстані від них (див. рис. 28). Позначимо через
містився на однаковій відстані від них (див. рис. 28). Позначимо через  відстань від фокуса до директриси, тоді фокус має координати
відстань від фокуса до директриси, тоді фокус має координати  ,
,  . Для довільної точки
. Для довільної точки  параболи відстань
параболи відстань  , а відстань до директриси
, а відстань до директриси  . За означенням
. За означенням 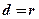 . З рис. 28 бачимо, що
. З рис. 28 бачимо, що  , а
, а  , тому
, тому

Рис. 28.


– канонічне рівняння параболи.
Парабола проходить через точку 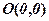 , яка називається її вершиною. Якщо точка
, яка називається її вершиною. Якщо точка  належить параболі, то і
належить параболі, то і 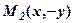 теж належить параболі, тому що із
теж належить параболі, тому що із

Отже, парабола симетрична відносно осі  , її графік достатньо побудувати в першій чверті, де із (42) випливає, що
, її графік достатньо побудувати в першій чверті, де із (42) випливає, що
 .
.
При  ця функція визначена для
ця функція визначена для  . При зростанні
. При зростанні 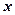 змінна
змінна  теж зростає. Графік зображено на рис. 29.
теж зростає. Графік зображено на рис. 29.

Рис. 29,а.
Рівняння директриси параболи  .
.
Парабола має “оптичну” властивість: якщо у фокусі параболи помістити джерело світла, то відбиті від параболи промені будуть паралельними осі  . Цю властивість враховують при виготовленні прожекторів, дзеркальних телескопів, теле- і радіоантен.
. Цю властивість враховують при виготовленні прожекторів, дзеркальних телескопів, теле- і радіоантен.
При додатному р рівняння

описує параболу симетричну відносно ОХ з вершиною в точці  , вітки якої напрямлені вліво (див. рис. 29,б)
, вітки якої напрямлені вліво (див. рис. 29,б)
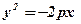

 Аналогічно викладеному, рівняння
Аналогічно викладеному, рівняння  і
і  описують параболи з вершиною в точці
описують параболи з вершиною в точці  симетричні відносно ОУ, вітки яких напрямлені відповідно вверх і вниз (див. рис. 29, в і г). Якщо, наприклад, рівняння
симетричні відносно ОУ, вітки яких напрямлені відповідно вверх і вниз (див. рис. 29, в і г). Якщо, наприклад, рівняння  розв’язати відносно у
розв’язати відносно у

і позначити  , то отримаємо відоме із шкільного курсу рівняння параболи
, то отримаємо відоме із шкільного курсу рівняння параболи 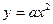 . Тепер її фокусна відстань
. Тепер її фокусна відстань  .
.
Задача 1. Знайти координати фокуса і скласти рівняння директриси параболи  .
.
Розв’язання. Порівнюючи канонічне рівняння  і дане
і дане  , отримуємо
, отримуємо  , тоді
, тоді  . Оскільки рівняння директриси
. Оскільки рівняння директриси  , то в даному випадку
, то в даному випадку  .
.
Задача 2. Скласти канонічне рівняння параболи а) з фокусом в точці  ; б) з фокусом в точці
; б) з фокусом в точці 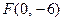 .
.
Розв’язання. а) Оскільки фокус  на додатній півосі ОХ, то парабола симетрична відносно ОХ з вершиною в точці
на додатній півосі ОХ, то парабола симетрична відносно ОХ з вершиною в точці  і
і  , тому
, тому  і згідно формули (42)
і згідно формули (42)
 .
.
б) Фокус 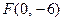 лежить на від’ємній півосі ОУ з вершиною в точці
лежить на від’ємній півосі ОУ з вершиною в точці  , вітки напрямлені вниз, канонічне рівняння слід шукати у вигляді
, вітки напрямлені вниз, канонічне рівняння слід шукати у вигляді  . Фокусна відстань параболи
. Фокусна відстань параболи  , і рівняння запишеться
, і рівняння запишеться
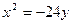 .
.
Задача 3. Показати шляхом виділення повного квадрата, що рівняння
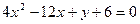
є рівнянням параболи. Звести його до канонічного вигляду. Знайти вершину, фокус, вісь і директрису цієї параболи.
Розв’язання. Виділимо відносно змінної х повний квадрат



 .
.
Позначимо  ,
, 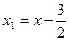 . Тоді внаслідок паралельного перенесення координатних осей в новий початок, тобто в точку
. Тоді внаслідок паралельного перенесення координатних осей в новий початок, тобто в точку  , отримаємо канонічне рівняння параболи
, отримаємо канонічне рівняння параболи
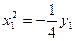 .
.
Вітки цієї параболи напрямлені вниз симетрично відносно осі  ,
,  - фокусна відстань. В новій системі координат фокус знаходиться в точці
- фокусна відстань. В новій системі координат фокус знаходиться в точці  , рівняння директриси в новій системі
, рівняння директриси в новій системі 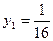 .
.
Повернемося до старих координат за допомогою заміни  ,
, 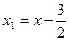 . Рівняння осі в новій системі
. Рівняння осі в новій системі  , а в старій
, а в старій  - рівняння осі параболи.
- рівняння осі параболи.
Рівняння директриси в новій системі координат 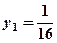 , а в старій
, а в старій  .
.
В новій системі  для фокуса
для фокуса 
 а в старій системі
а в старій системі  ;
; 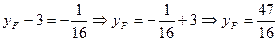 , тобто
, тобто  .
.
1. Знайти координати фокуса і записати рівняння директриси для поданих парабол: 1)  ; 2)
; 2)  ; 3)
; 3)  ; 4)
; 4)  .
.
2. Скласти канонічне рівняння параболи, якщо відомо, що:
а) парабола має фокус 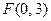 і вершину
і вершину  ;
;
б) парабола симетрична відносно осі абсцис і проходить через точки  і
і  ;
;
в) парабола симетрична відносно осі ординат і проходить через точки  і
і 
3. Рівняння директриси параболи  . Скласти канонічне рівняння цієї параболи, якщо її вершина в точці
. Скласти канонічне рівняння цієї параболи, якщо її вершина в точці  . Знайти координати фокуса.
. Знайти координати фокуса.
4. На параболі  взята точка А(х,у), яка знаходиться від директриси на відстані
взята точка А(х,у), яка знаходиться від директриси на відстані  . Знайти відстань цієї точки від вершини параболи.
. Знайти відстань цієї точки від вершини параболи.
5. Знайти фокальний радіус точки В параболи  , якщо її абсциса дорівнює 8.
, якщо її абсциса дорівнює 8.
6. Знайти точки перетину параболи  з прямими: а)
з прямими: а)  ; б)
; б)  ; в)
; в)  .
.
7. Знайти координати вершини і фокуса, скласти рівняння осі і директриси кожної із поданих парабол: а) 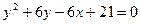 ; б)
; б)  ; в)
; в)  ; г)
; г) 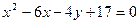 .
.
8. Вісь симетрії параболи паралельна осі ординат, а рівняння директриси  . Скласти рівняння параболи, якщо вона перетинає вісь ОХ в точках (-5, 0) і (11, 0).
. Скласти рівняння параболи, якщо вона перетинає вісь ОХ в точках (-5, 0) і (11, 0).
9. Через фокус параболи  проведені дві прямі, одна з яких складає з віссю ОХ кут
проведені дві прямі, одна з яких складає з віссю ОХ кут  , а друга -
, а друга - 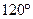 . Точки перетину цих прямих з параболою послідовно з’єднані між собою. Знайти площу утвореного чотирикутника.
. Точки перетину цих прямих з параболою послідовно з’єднані між собою. Знайти площу утвореного чотирикутника.
10. Діаметр кругової параболічної антени 60см, глибина її 7,5. На якій відстані від вершини параболи необхідно поставити уловлювач сигналів, щоб відбиті сигнали від супутника перетинались у цій точці (вважається, що сигнали, які напрямлені на антену від супутника йдуть паралельно осі антени).
11. Тіло, кинуте під кутом до горизонту, описало дугу параболи і упало на відстані 32м від початкового положення. Знайти параметр параболічної траєкторії та записати рівняння, якщо найбільша висота досягнута тілом, дорівнює 12м.
Відповіді: 1. 1)  ; 2)
; 2)  ; 3)
; 3) 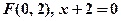 ; 4)
; 4)  . 2. а)
. 2. а)  ; б)
; б)  ; в)
; в)  .
.
3. 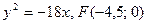 . 4.
. 4.  . 5. 14.
. 5. 14.
6. а)  ; б)
; б)  ; в)
; в)  . 7. а)
. 7. а) 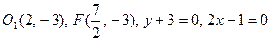 ; б)
; б) 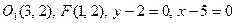 ; в)
; в)  ; г)
; г)  . 8.
. 8.  або
або 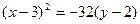 . 9.
. 9.  . 10. 30. 11.
. 10. 30. 11. 
|
|
|
|
|
Дата добавления: 2017-01-14; Просмотров: 560; Нарушение авторских прав?; Мы поможем в написании вашей работы!