Потенциальное течение жидкости

Стационарное температурное поле

При изучении уравнения теплопроводности было установлено, что температура нестационарного теплового поля удовлетворяет уравнению

.

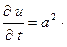
Если процесс стационарен, то и, таким образом, устанавливается распределение температуры 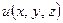, удовлетворяющее уравнению Лапласа .

Если требуется получить распределение температуры в некоторой области, ограниченной поверхностью Г, то к этому уравнению следует присоединить граничные условия:

- на Г (заданное распределение температуры на границе);

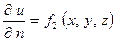- на Г (заданный тепловой поток через границу).

Рассмотрим движение идеальной жидкости, характеризующееся скоростью 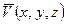. Выделим в жидкости некоторую неподвижную замкнутую поверхность произвольной формы (рис. 5) и рассмотрим массу жидкости, вытекающей за единицу времени из замкнутой поверхности .

Эта масса выражается поверхностным интегралом , где 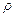- плотность жидкости, - нормальная составляющая скорости. Истечение жидкости из замкнутой поверхности повлечет за собой уменьшение плотности в точках внутри за единицу времени на величину 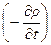и соответствующее изменение массы жидкости внутри поверхности, равно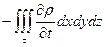е , где - пространство, ограниченное поверхностью .

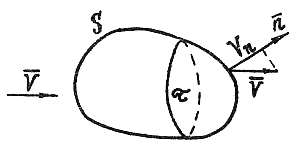
Рис. 5

Поскольку масса сохраняется, то

= ,

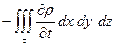преобразуя поверхностный интеграл по формуле Остроградского, получим

.

Теперь

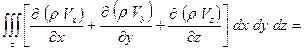
или

.

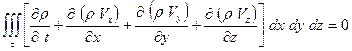Вследствие произвольности объема приходим к уравнению

,

которое называется уравнением неразрывности.

Если жидкость несжимаема (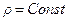) и движение стационарно 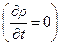, то уравнение неразрывности принимает вид

. 44)

Предположим, что движение жидкости потенциальное. Это значит, что скорость является градиентом некоторой функции

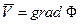, 45)

называемой потенциалом скорости. Равенство 45) равносильно следующим трем 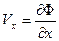, , . Таким образом, приходим к уравнению Лапласа .

Если жидкость обтекает границу Г, представляющую собой твердую непроницаемую стенку, то нормальная составляющая скорости равна нулю, что приводит к граничному условию 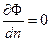на Г.

К уравнению Лапласа сводятся также многочисленные задачи теории упругости, электростатики, магнитостатики и др.

Дата добавления: 2015-07-13