
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Решение задачи Дирихле методом конечных разностей
|
|
|
|
Решение краевых задач методом разделения переменных
Уравнение Лапласа в полярных координатах
При решении многочисленных задач математической физики часто используется двумерное уравнение Лапласа
 , 46)
, 46)
решение, которого часто выгоднее искать в полярных координатах.
Преобразуем уравнение 46) к полярным координатам, положив
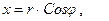
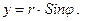
Дифференцируя по правилу дифференцирования сложной функции
 ,
,  ,
,
но
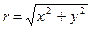 ,
, 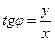 ,
,
а тогда
 ,
,  ,
,
 ,
,
аналогично 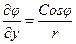 .
.
Теперь
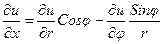 ,
, 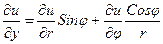 .
.
Применяя правило дифференцирования сложной функции к производным  и
и 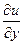 , найдем вторые частные производные
, найдем вторые частные производные
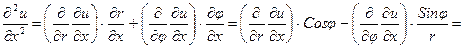


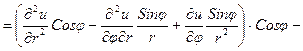


 ,
,
аналогично


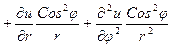 .
.
Теперь 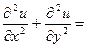

 .
.
Таким образом, уравнение Лапласа в полярных координатах имеет вид

 . 47)
. 47)
Решение краевых задач для уравнения Лапласа может быть найдено методом разделения переменных в случае некоторых простейших областей (прямоугольник, круг, сектор и др.). При решении конкретных задач обычно пользуются общим решением уравнения Лапласа, которое получается методом разделения переменных и имеет вид:
- в полярных координатах
 ; 48)
; 48)
- в декартовых координатах
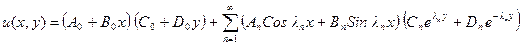 . 49)
. 49)
Неопределенные коэффициенты 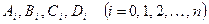 и
и 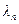 определяются из граничных условий и физического смысла задачи.
определяются из граничных условий и физического смысла задачи.
2.3.4.1. Решение уравнения Лапласа в кольце
Найдем решение уравнения Лапласа в кольце, ограниченном окружностями 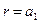 и
и  и принимающее следующие граничные значения
и принимающее следующие граничные значения
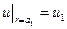 ,
, 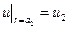 , 50)
, 50)
где  ,
,  - постоянные.
- постоянные.
Для решения поставленной задачи воспользуемся соотношением 48). Удовлетворяя первому граничному условию из 50), получим
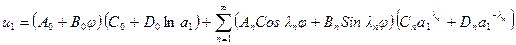 ,
,
так как здесь левая часть не зависит от 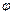 , то в правой следует положить
, то в правой следует положить 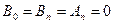 . И теперь решение имеет вид
. И теперь решение имеет вид
 . 51)
. 51)
Таким образом, удовлетворение граничным условиям 50) приводит к
следующей системе для отыскания неизвестных коэффициентов 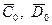 :
:

откуда находим
 ,
,  .
.
Подставляя найденные значения 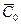 и
и 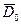 в формулу 51) окончательно получим решение сформулированной задачи для кольца:
в формулу 51) окончательно получим решение сформулированной задачи для кольца:
 .
.
2.3.4.2. Решение задачи Дирихле для полуполосы
Требуется найти решение уравнения Лапласа внутри полуполосы (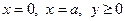 ), удовлетворяющее граничным условиям:
), удовлетворяющее граничным условиям:
- 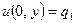 ,
,  ;
;
-  ,
, 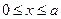 ;
;
- 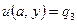 ,
,  ,
,
где  ,
, 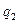 ,
,  - постоянные.
- постоянные.
Для решения задачи воспользуемся соотношением 49). Решение задачи должно быть ограниченным при 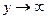 , поэтому в 49) следует положить
, поэтому в 49) следует положить  :
:
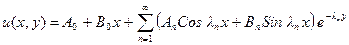 ,
,
здесь 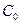 включено в
включено в 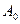 и
и 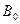 , а
, а 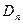 - в
- в 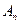 и
и 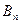 .
.
Определим 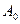 ,
,  из первого граничного условия:
из первого граничного условия:
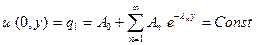 ,
,
откуда  ,
, 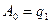 , следовательно,
, следовательно,
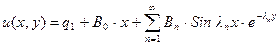 .
.
Из третьего граничного условия получаем:
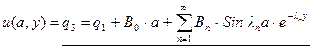 ,
,
откуда  и
и 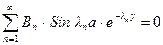 , или
, или 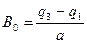 ,
,  . Теперь искомое решение
. Теперь искомое решение
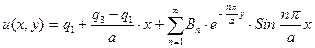 . 52)
. 52)
Коэффициенты  определятся из второго граничного условия
определятся из второго граничного условия
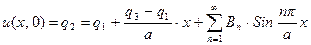 ,
,
или  .
.
В последнем соотношении известная линейная функция, стоящая в левой части представлена (в правой части) в виде разложения в ряд Фурье по синусам кратных дуг на интервале  .
. 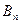 - коэффициенты Фурье этого разложения, они вычисляются по формулам
- коэффициенты Фурье этого разложения, они вычисляются по формулам
 . 53)
. 53)
Таким образом, сформулированная задача имеет решение 52) - 53).
Пусть требуется найти решение уравнения Лапласа

в плоской замкнутой области 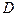 с границей Г (рис. 6), удовлетворяющее граничному условию
с границей Г (рис. 6), удовлетворяющее граничному условию
 на Г,
на Г,
где  - заданная непрерывная функция.
- заданная непрерывная функция.

Рис. 6
Для решения сформулированной задачи проведем два семейства прямых
 ,
, 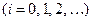 ;
;  ,
,  ,
,
где  - заданное число. Будем говорить, что область
- заданное число. Будем говорить, что область 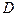 покрыта сеткой. Приближенное значение искомой функции в точке
покрыта сеткой. Приближенное значение искомой функции в точке 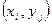 обозначим
обозначим 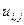 . Аппроксимируем заданную область
. Аппроксимируем заданную область 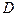 сетчатой областью
сетчатой областью  , состоящей из всех квадратов, целиком лежащих в области
, состоящей из всех квадратов, целиком лежащих в области 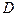 и некоторых пересекаемых границей Г. При этом контур Г аппроксимируется контуром Г
и некоторых пересекаемых границей Г. При этом контур Г аппроксимируется контуром Г  . В каждом узле, лежащем на контуре Г
. В каждом узле, лежащем на контуре Г  , зададим значение
, зададим значение  , равное значению функции
, равное значению функции 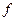 в ближайшей точке контура Г. Значения искомой функции будем рассматривать только в узлах сетки. Заменим производные, входящие в уравнение Лапласа, конечными разностями:
в ближайшей точке контура Г. Значения искомой функции будем рассматривать только в узлах сетки. Заменим производные, входящие в уравнение Лапласа, конечными разностями:
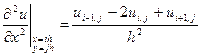 ,
,  .
.
Уравнение Лапласа заменится следующим уравнением в конечных разностях  , или, сокращая на
, или, сокращая на 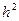 и разрешая относительно
и разрешая относительно  , получим:
, получим:
 . 54)
. 54)
Уравнения 54) составляются для каждого узла сетки, лежащего внутри области  и не лежащего на границе Г
и не лежащего на границе Г  . Если точка
. Если точка 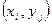 соседняя с точкой контура Г
соседняя с точкой контура Г  , то в правой части 54) будут известные значения
, то в правой части 54) будут известные значения  .
.
Таким образом, получаем неоднородную систему N уравнений с N неизвестными, где N – число узлов сетки, лежащих внутри области  . Доказывается, что полученная система имеет решение и притом единственное. Определенные из системы 54) значения
. Доказывается, что полученная система имеет решение и притом единственное. Определенные из системы 54) значения  - приближенные решения сформулированной задачи Дирихле в точках построенной сетки.
- приближенные решения сформулированной задачи Дирихле в точках построенной сетки.
ЗАКЛЮЧЕНИЕ
Уравнения математической физики отражают общие черты, свойственные тем или иным процессам. Особенности конкретного процесса устанавливаются условиями однозначности, которые состоят из геометрических, физических, временных и граничных условий. Геометрические условия содержат информацию о форме и размерах тела. Физические условия дают значения физических величин участвующих в процессе. Временные и граничные условия, объединяемые под общим названием краевых условий, указывают на особенности протекания процесса во времени и на границах тела. Математически сформулированная задача содержит дифференциальное уравнение и краевые условия.
Среди различных способов решения уравнений математической физики можно выделить аналитические, численные, графические и решение с помощью аналогов. С бурным развитием вычислительной техники последние два способа (графические и с помощью аналогов) стали иметь меньшее применение. Аналитические методы можно разделить на точные и приближенные. Для решения задач часто применяются метод разделения переменных и операционный способ. Из приближенных аналитических методов следует отметить интегральный и вариационные методы. Наиболее ценными методами численного решения таких уравнений является метод конечных разностей (метод сеток) и метод конечного элемента, которые позволяют найти решение в отдельных точках области искомого решения.
ЛИТЕРАТУРА
- Численные методы решения физических задач: учеб. пособие / В. И. Ращиков, А. С. Рошаль. - СПб.; М.; Краснодар: Лань, 2005. - 208 с.
- Поршнев С. В. Вычислительная математика. Курс лекций: Учеб. пособие / С. В. Поршнев. - СПб.: БХВ-Петербург, 2004. - 320 с.
- Губенков А. А. Методы конечных и граничных элементов. Теоретические основы математического моделирования твердотельных упругих устройств / А.А. Губенков; Сарат. гос. техн. ун-т; Сарат. гос. техн. ун-т (Саратов). - Саратов: СГТУ, 2006. - 167 с.
- Колокольцев В. А. Основы применения метода конечных элементов в расчетах деталей машин: учеб. пособие по курсу "Детали машин"для студ. машиностроит. спец. / В. А. Колокольцев; Сарат. гос. техн. ун-т (Саратов). - Саратов: СГТУ, 2003. - 84 с.
- Бочкарев А.В. Уравнения эллиптического типа и специальные функции: Учеб.пособие / А.В. Бочкарев, П.Б. Федоров. - Саратов: СГТУ, 2008. - 72 с.
- Емельянов В. М. Уравнения математической физики: практикум по решению задач: Учеб. пособие / В. М. Емельянов, Е. А. Рыбакина. - СПб.; М.; Краснодар: Лань, 2008. - 224 с.
- Сабитов К. Б. Уравнения математической физики: Учеб. пособие / К. Б. Сабитов. - М.: Высшая школа, 2003. - 255 с.
- Тихонов А.Н. Уравнения математической физики: Учеб. пособие / А.Н. Тихонов, А.А. Самарский. – М.: МГУ, 2007. – 798 с.
- Арсенин В.Я. Методы математической физики и специальные функции: Учеб.пособие / В. Я. Арсенин. - 2-е изд., перераб.и доп. - М.: Наука, 1984. - 384 с.
- Годунов С. К. Уравнения математической физики: Учеб.пособие / С. К. Годунов. - 2-е изд., исправл. и дополн. - М.: Наука, 1979. - 392 с.
- Владимиров В.С. Уравнения математической физики: Учебник / В. С. Владимиров. - 5-е изд., доп. - М.: Наука, 1988. - 512 с.
- Бидасюк Ю.М. Mathsoft MathCAD 11: Самоучитель / Ю. М. Бидасюк. - М.; СПб.; Киев: Диалектика, 2004. - 224 с.
- Глушаков С.В. Математическое моделирование: Mathcad 2000. Matlab 5; учебный курс / С. В. Глушаков, И. А. Жакин, Т. С. Хачиров. - Москва: АСТ; Харьков: Фолио, 2001. - 524 с.
- Дьяконов В. Mathcad 8/2000: Спец.справочник / В. Дьяконов. - СПб.: Питер, 2001. - 592 с.
- Линьков В.М. Высшая математика в примерах и задачах. Компьютерный практикум: учеб. пособие / В. М. Линьков, Н. Н. Яремко; ред. А. А. Емельянов. - М.: Финансы и статистика, 2006. - 320 с.
- Мэтьюз Д.Г. Численные методы. Использование MATLAB / Д. Г. Мэтьюз, К. Д. Финк; пер. с англ. под ред. Ю. В. Козаченко. - 3-е изд. - М., СПб., К.: Изд. дом "Вильямс", 2001. - 720 с.
- Потемкин В.Г. Введение в MATLAB: Учебно-справочное изд. / В. Г. Потемкин. - М.: Диалог-МИФИ, 2000. - 247 с.
- Третьяков С.А. Некоторые численные методы прикладной электродинамики: учеб. пособие / С.А. Третьяков, А.С. Черепанов, Ю.Н. Новиков. - СПб.: СПбГТУ, 1993. - 64 с.
- Черняк А. А. Высшая математика на базе Mathcad. Общий курс: учеб. пособие / А.А. Черняк, Ж.А. Черняк, Ю.А. Доманова. - СПб.: БХВ-Петербург, 2004. - 608 с.
- Вельмисов П. А. Уравнения математической физики: Учеб. пособие для студ. всех спец. техн. вузов / П.А. Вельмисов. - Ульяновск: УлПИ, 1994. - 75 с.
|
|
|
|
|
Дата добавления: 2015-07-13; Просмотров: 2545; Нарушение авторских прав?; Мы поможем в написании вашей работы!