Краткая теория из курса алгебры

Пусть дана система линейных уравнений (1). Матричный способ решения систем линейных уравнений используется в тех случаях, когда число уравнений равно числу переменных.

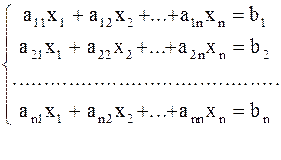(1)

Введем обозначения. Пусть А – матрица коэффициентов при переменных, B – вектор свободных членов, X – вектор значений переменных. Тогда X = A^-1 × B, где А^-1 – матрица, обратная А. Причем обратная матрица А^-1 существует, если определитель матрицы А не равен 0. Произведение исходной матрицы А и обратной А^-1 должно быть равно единичной матрице:

А^-1А=АА^-1=Е.

Задание: Решить систему линейных уравнений:

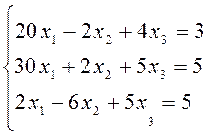
Технология работы:

Пусть на диапазоне А11:С13, задана исходная матрица А, составленная из коэффициентов системы. Сначала найдите определитель матрицы А. Для этого в ячейке F15 необходимо выбрать команду Вставить функцию на вкладке Формулы. В категории " Ссылки и массивы " найдите функцию МОПРЕД(), задайте ее аргумент A11:С13. Получили результат 344. Так как определитель исходной матрицы А не равен 0, т.е. существует обратная ей матрица, поэтому следующим этапом и будет нахождение обратной матрицы. Для этого выделите диапазон А15:С17, где будет размещаться обратная матрица. Вызвав Мастера функций, в категории " Ссылки и массивы " найдите функцию МОБР(), задайте ее аргумент A11:С13 и нажмите Shift+Ctrl+Enter. Чтобы проверить правильность обратной матрицы, умножьте ее на исходную с помощью функции МУМНОЖ(). Вызовите эту функцию, предварительно выделив диапазон А19:А21. В качестве аргументов укажите исходную матрицу А, т.е. диапазон А11:С13 и обратную матрицу, т.е. диапазон А15:С17 и нажмите Shift+Ctrl+Enter. Получили единичную матрицу. Таким образом, обратная матрица найдена верно. Теперь для нахождения результата, выделите для него диапазон F18:F20. Вызовите функцию МУМНОЖ(), используя Мастера функций, укажите два массива-диапазона, которые будете перемножать − обратную матрицу и столбец свободных членов, т.е. А15:С17 и Е11:Е13 и нажмите Shift+Ctrl+Enter. Результат показан на рисунке 10.

Теперь можно произвести проверку правильности найденных решений х₁, х₂ и х₃. Для этого, выполните вычисление каждого уравнения, используя найденные значения х₁, х₂ и х₃. Например, в ячейке G11 подсчитайте значение , при этом результат должен быть равен 3. Введем следующую формулу =A11*$F$18+B11*$F$19+C11*$F$20.

Скопируйте эту формулу в две ячейки, расположенные ниже, то есть в G12 и G13. Снова получите столбец свободных членов. Таким образом, решение системы линейных уравнений выполнено верно.

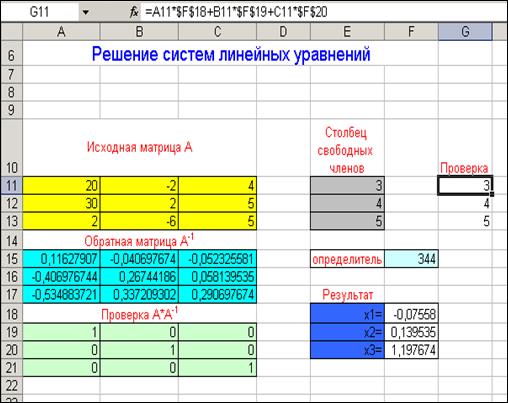
Рисунок 10 - Решение системы линейных уравнений

Задание 5. Транспортная задача

Есть три поставщика с мощностями с1, с2, с3 и пять потребителей (их спрос d1, d2, d3, d4, d5 соответственно) некоторого груза. Стоимость доставки единицы груза от каждого поставщика к каждому потребителю задается матрицей А размера 3х5. Необходимо составить план перевозок по доставке требуемой продукции в пункты распределения, минимизирующий суммарные транспортные расходы.

№ Варианта
с1
c2
c3
d1
d2
d3
d4
d5
a11
a12
a13
a14
a15
a21
a22
a23
a24
a25
a31
a32
a33
a34
a35

№ Варианта
с1
c2
c3
d1
d2
d3
d4
d5
a11
a12
a13
a14
a15
a21
a22
a23
a24
a25
a31
a32
a33
a34
a35

Пример оформления

В ячейки B4:F6 (рисунок 12) заносится матрица цен, далее в ячейки B11:F13 помещаются любые значения больше нуля. В ячейках G11:G13, вычисляются суммы ячеек B11:F11; B12:F12; B13:F13 соответственно. В B14:F14, вычисляются суммы ячеек B11:B13; C11:C13; D11:D13; E11:E13; F11:F13 соответственно. В ячейку F16 записывается следующая формула: =СУММПРОИЗВ(B11:F13;B4:F6), вычисляющая произведение соответствующих элементов массивов, а затем суммирует получившиеся значения.

Далее выделив ячейки B11:F13 в контекстном меню вызываем Формат ячеек и во вкладке Число, для числового формата данных выставляем число десятичных знаков равным нулю.

Средство Поиск решения на вкладке Данные вгруппе команд Анализ ( если данная команда не подключенанужно подключитьнадстройку Пакет анализа:в меню Файл выбрать команду Параметры→Надстройки) найдет оптимальный план поставок продукции и соответствующие ему транспортные расходы.

Оформим окно поиска решений как показано на рисунке 11:

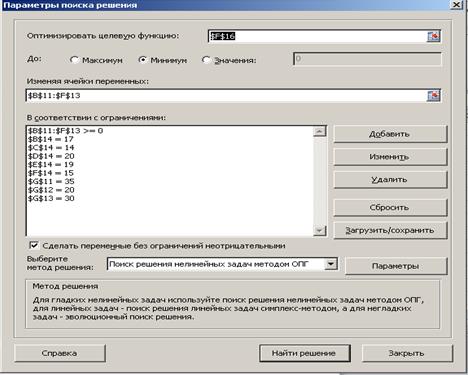
Рисунок 11 – Окно «Параметры поиска решения»

1. Оптимизировать целевую функцию - $F$16

2. До: Минимума

3. Изменяя ячейки переменных: $В$11:$F$13

4. В соответствии с ограничениями:

$В$11:$F$13 >= 0

$В$14 = 17

$C$14 = 14

$D$14 = 20

$E$14 = 19

$F$14 = 15

$G$11 = 35

$G$12 = 20

$G$13 = 30

	A	B	C	D	E	F	G
		Потребитель 1	Потребитель 2	Потребитель 3	Потребитель 4	Потребитель 5
	Поставщик 1
	Поставщик 2
	Поставщик 3
		Потребитель 1	Потребитель 2	Потребитель 3	Потребитель 4	Потребитель 5
	Поставщик 1
	Поставщик 2
	Поставщик 3

Рисунок 12 – Решение транспортной задачи

Итак из ячейки F16 мы видим, что минимальные затраты на перевозку составляют: 453 ед.

А в ячейках B11:F13 был получен план грузоперевозок.

Дата добавления: 2015-07-13