Задачи с решениями

Задачи по теме «Равномерное движение. Сложение скоростей. Относительность движения»

1. Человеку необходимо перейти поле и переплыть реку за кратчайшее время. До реки 1 км, ширина реки 100 м, река прямая. Скорость передвижения человека по полю 5 км/час, по воде (относительно воды) 1 км/час. Скорость течения реки относительно берегов 5 км/час. Найти минимальное время движения. Найти модуль вектора перемещения человека в этом случае. Как нужно двигаться человеку, чтобы модуль вектора перемещения был минимальным? Найти его.

Решение:

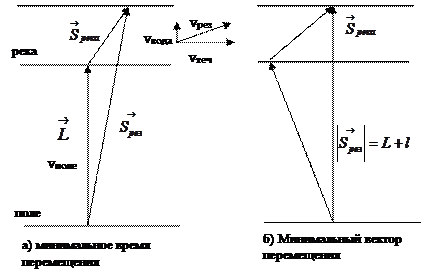а) минимальное время движения (рисунок)

Минимальное время движения достигается, когда скорость человека и при движении по полю, и при движении по реке, направлена перпендикулярно берегу реки. В этом случае

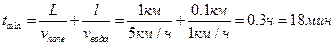
Вектор перемещения в данном случае определяется из соотношения:

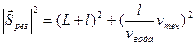
б) минимальный вектор перемещения

Минимальный вектор перемещения – перпендикуляр из исходной точки положения человека к противоположному берегу реки (рисунок). Человек должен идти по берегу так, чтобы компенсировать дальнейший снос рекой при плавании. Возможный вариант – по полю двигаться под некоторым углом α к перпендикуляру к берегу, а в воде двигаться перпендикулярно берегу. Тогда α определяется из соотношения:

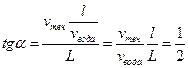
Есть и второе решение. Найдите его.

2. Обское море ранее было прямой рекой. Чартерный пароход «Обь» совершал рейс по реке от Новосибирска до Камня - на Оби и обратно за время t, а сейчас по морю за время T. Сравнить t и T (<,>,=?)

Решение:

Пусть расстояние от Новосибирска до Камня - на Оби равно 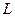, скорость течения 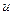, скорость парохода относительно воды 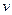. Пароход за один рейс проходит путь (и по реке, и по морю).

а) Когда пароход двигался по реке, при движении «туда» скорость парохода относительно берегов была , при движении «обратно» 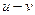. Таким образом, полное время движения парохода туда-обратно по реке:

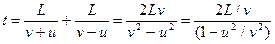
б) Когда построили водохранилище, исчезло течение. То есть пароход стал двигаться равномерно в прямом и обратном направлении с одинаковой скоростью 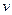. Тогда время его движения по морю:

.

Поскольку 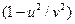<1, .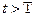

3. Метеорит, летящий со скоростью 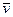, после подрыва разрывается на два одинаковых осколка. На каком минимальном расстоянии от Земли нужно сделать подрыв, чтобы осколки пролетели мимо. Относительная скорость осколков 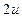. Считать, что после подрыва поле Земли практически не меняет скорости осколков. Радиус Земли R. Вектор 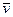проходит через центр Земли.

Решение:

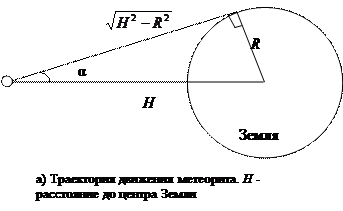
Метеорит двигался равномерно. Его скорость была направлена к центру Земли. После взрыва (рисунок а) траектория движения осколков должна стать такой, чтобы касаться Земли в некоторой точке (из условия минимальности расстояния от Земли до точки подрыва). Тогда угол

между исходной траекторией метеорита и траекторией осколка:. .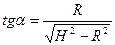

До взрыва метеорит имел скорость 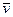, направленную к центру Земли. После взрыва осколки метеорита сохранили эту компоненту скорости. Кроме того, у осколков возникла компонента скорости ± u, перпендикулярная исходной скорости 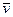(рисунок б). При равномерном движении вектор скорости и перемещения сонаправлены, поэтому можно записать:

.

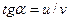Поскольку 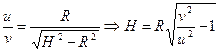- расстояние от точки подрыва до центра Земли.

4. На круговом конвейере двигаются сумки (в аэропорту). В поисках своей сумки студент ФЕН, пройдя рядом с конвейером в одну сторону пять кругов, насчитал 400 сумок, пять кругов в обратную – 600. Сумки не снимали и дополнительно не ставили. Сколько всего было сумок на конвейере? Найти скорость конвейера. Скорость студента 5 км/час.

Решение:

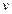Студент идет вдоль конвейера равномерно. Конвейер также движется равномерно. Время движения вдоль конвейера (прохода пяти кругов) не меняется при включении конвейера. Пусть плотность сумок на конвейере составляет сумок на метр, всего на конвейере количество сумок , скорость студента , скорость конвейера 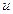. Тогда длина конвейера 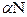, время движения студента в ту и другую сторону при проходе пяти кругов 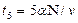, одного круга 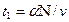. В единицу времени при движении вдоль покоящегося конвейера студент насчитывает сумок 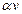, при движении по ходу движущегося конвейера насчитывает сумок 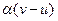, при движении в обратную сторону насчитывает сумок . Тогда 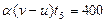; . Из последних соотношений получаем 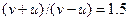, и, поскольку 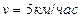, находим , а также . Всего сумок на конвейере 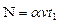. Поскольку 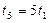, находим .

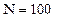Задачи по теме «Движение с ускорением, движение в поле тяжести»

5. Из пушки стреляют и попадают по цели, находящейся на расстоянии L=1 км по горизонтали. С какой минимальной скоростью нужно выпустить снаряд? Сопротивление воздуха не учитывать. Какова будет максимальная высота H подъема снаряда? Найти минимальное и максимальное значения нормального, тангенцального и полного ускорения тела при движении по траектории.

Решение:

Время полета снаряда .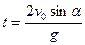

Здесь - начальная скорость, 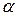- угол вылета снаряда по отношению к горизонту.

Расстояние, пройденное по горизонтали .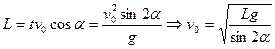

Следовательно, минимальная скорость будет при 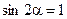. При этом 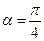. Тогда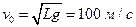

Максимальная высота подъема .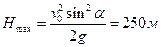

Полное ускорение в любой точке равно g. 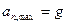в верхней точке. 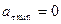в верхней точке.

6. Из пушки делают два одинаковых выстрела с интервалом 4 секунды. Первый снаряд ударяется в землю через 6 секунд после того, как второй снаряд проходит верхнюю точку траектории. Расстояние от пушки до места падения снарядов 5 километров. Найти минимальное расстояние между снарядами в полете.

Решение:

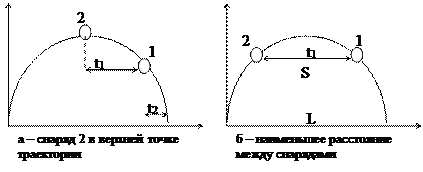
Начальные условия одинаковы, поэтому снаряды летят по одинаковой траектории. От момента прохождения верхней точки траектории вторым снарядом до его падения на землю проходит время 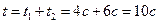, где 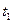– время задержки между выстрелами, 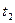– время до падения первого снаряда, осчитываемое от момента прохождения вторым снарядом верхней иточки траектории. Это половина всего времени полета каждого снаряда. Полное время дижения каждого снаряда от выстрела до падения соответственно равно 20 с. Используя эти данные, найдем 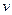- горизонтальную составяющую скорости снарядов:

= 250 м/с.

Расстояние между снарядами складывается из двух компонент – по горизонтали и по вертикпли. Пока оба снаряда в полете, горизонтальная компонента не меняется. Потому минимальное расстояние между снарядами будет в тот момент, когда оба они будут на одной высоте (рисунок б). Отсюда определяем искомое минимальное расстояние:

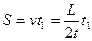=1 км.

7. На высоте H от земли горизонтально подвешена труба длиной l. Тело бросают с земли так, что оно влетает в трубу горизонтально, и, скользя в ней, останавливается у конца трубы. Коэффициент трения в трубе m. Определить величину начальной скорости тела .

Решение:

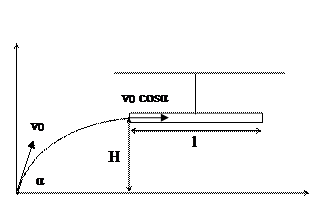В верхней точке траектории тело будет иметь только горизонтальную скорость 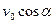. Из формулы для максимальной высоты подъема 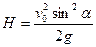найдем, что

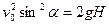(1)

В трубе тело двигалось равнозамедленно. При этом кинетическая энергия тела перешла в работу силы трения:

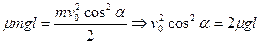(2)

Решая систему уравнений (1) и (2) относительно v₀ и cosα, найдем:

.

Задачи по теме «Законы Ньютона»

8.По наклонной плоскости (угол альфа) с постоянной скоростью съезжает доска массы М. Сверху доски находится тело массы m. Тело m удерживается на одном месте нитью, привязанной где-то сверху так, что нить параллельна доске. Найти коэффициент трения между телом m и доской. Между доской и наклонной плоскостью трения нет.

Решение:

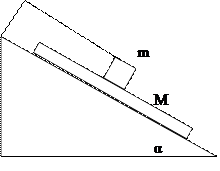Так как доска М имеет постоянную скорость, 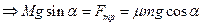Таким образом, находим коэффициент трения .

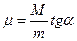9. На горизонтальной плоскости лежит монета. Плоскость начинают двигать с ускорением в горизонтальном направлении. При каком минимальном ускорении монета начнет скользить по плоскости? Коэффициент трения m. Рассмотреть также общий случай наклонной плоскости (угол к горизонту b). Во втором случае вектор ускорения перпендикулярен полю тяжести g и нормали к плоскости.

Решение:

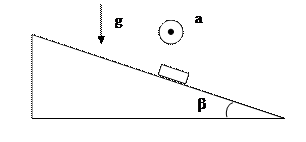
Пусть доска движется с ускорением а, при этом монета скользит по доске. Тогда под действием силы трения монета двигается с ускорением b, определяемым из соотношения μmg = mb. Если уменьшать ускорение а, монета перестанет скользить при условии

.

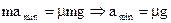На монету, лежащую на наклонной плоскости, действует скатывающая сила mg×sinβ и сила трения. Если при движении (ускорении а) наклонной плоскости монета относительно плоскости не скользит, сила трения определяется из соотношения:

Из этого соотношения видно, что при увеличении ускорения плоскости сила трения растет. Максимальная сила трения:

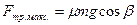
Условием начала движения монеты относительно плоскости будет равенство:

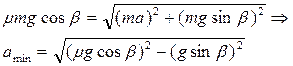
10. На веревке, перекинутой через блок, уравновешены два одинаковых груза, массы m каждый. Половину одного груза перекладывают на другой груз и систему отпускают. Найти натяжение веревки в первом и во втором случае. Веревка невесома и нерастяжима, трения нет. Как изменится ответ в реальном случае?

Решение:

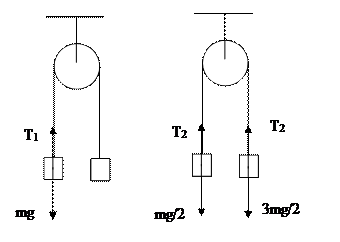
В первом случае, когда массы грузов равны, система покоится. Сила натяжения каждой нити .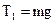

Для второго случая запишем второй закон Ньютона для каждого тела. Учтем, что нить нерастяжима и невесома, поэтому сила натяжения нити справа и слева от блока одинаковы, и ускорения, с которым движутся тела, по модулю равны между собой.

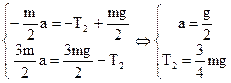
10. Как должен двигаться студент ФЕН по горизонтальной поверхности с привязанной на веревочке консервной банкой, чтобы эта банка не ударялась о землю. Длина веревочки L больше высоты студента H. Трения тел о воздух нет. Прим.: задача имеет несколько решений.

Решение:

а) Студент может бежать с ускорением.

Перейдем в систему отсчета, связанную со студентом и банкой. Чтобы банка была неподвижна, действие сил на нее должно быть скомпенсировано. На банку действуют следующие силы: сила тяжести mg, сила натяжения нити Т и, поскольку студент, двигающийся с ускорением, является неинерциальной системой отсчета, сила инерции .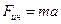

Сумма сил, действующих на банку в системе отсчета «студент» равна нулю. Составляющая силы натяжения уравновешивается силой тяжести mg. А составляющая силы натяжения 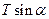- силой инерции. 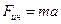: 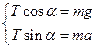. Поделим нижнее уравнение на верхнее. Тогда .

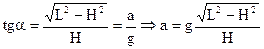б) студент может равномерно бежать по окружности радиуса R с некоторой скоростью v.

Решение в этом случае аналогично.

в) студент может вращать банку относительно себя.

11. После удара шайба скользит по льду и через время t останавливается, пройдя расстояние L. Найти коэффициент трения.

Решение:

После удара шайба останавливается под действием силы трения. По второму закону Ньютона 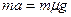. Поэтому ускорение шайбы 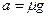, начальная скорость .

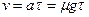Зависимость пути от времени при равнозамедленном движении от начальной скорости 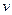до остановки , .

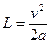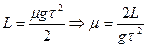Задачи по теме «Законы сохранения энергии и импульса»

12. Тело падает и отскакивает вертикально с высоты 2 м до высоты 1 м. Как меняется импульс тела при отскоке? Сколько энергии переходит в тепло? Масса тела 1 кг.

Решение:

Измнеие импульса тела ,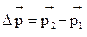

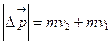
Скорости тела перед падением и после отскока найдем из закона сохранения энергии: 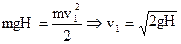. Аналогично, 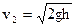. Тогда изменение импульса равно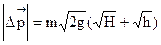

Чтобы найти, сколько энергии перешло в тепло, еще раз используем закон сохранения энергии: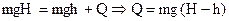

13. Пуля массы m, летящая вертикально вверх со скоростью v, застревает в доске массы M, лежащей на двух опорах. Определить количество теплоты, которое выделилось при этом, и высоту, на которую поднялись пуля и доска.

Решение:

Запишем закон сохранения импульса и энергии для момента, когда пуля застревает в доске:

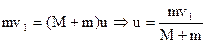
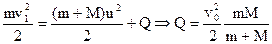
Высоту подъема доски с застрявшей пулей найдем из закона сохранения энергии:

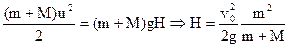
14. На сортировочной станции на покоящийся вагон массы m с горки направляют вагон с массы 2m. Как отличаются скорости вагонов до и после сцепки? Какая часть кинетической энергии системы переходит в тепло при сцепке? Вагоны, в конце концов, останавливаются. Почему не сохраняется суммарный импульс двух вагонов?

Решение:

До сцепки вагон массы 2m имеет скорость v₁. Второй вагон имеет нулевую скорость. После сцепки вагоны движутся с одинаковой скоростью v₂.

Запишем закон сохранения импульса , тогда можно выразить соотношение скоростей вагонов до и после сцепки как .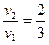

Количество энергии, перешедшей в тепло, найдем по закону сохранения энергии с учетом соотношения скоростей:

. То есть 1/3 начальной кинетической энергии перешла в тепло.

После сцепки суммарный импульс не сохраняется, потому что на вагоны действует внешняя сила – сила трения.

15. Горизонтально летящей со скоростью V пулькой пробивают брусок, стоящий на краю вертикального обрыва высоты Н. Брусок падает на расстоянии A от основания обрыва, пулька - на расстоянии Б. Во сколько раз масса пульки меньше массы бруска?

Решение:

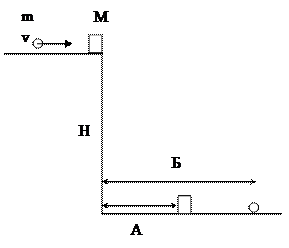После того, как пулька пробьёт брусок, они будут иметь только горизонтальную скорость, поэтому на Землю упадут одновременно, но будут лететь по разным траекториям. Запишем закон сохранения импульса для момента, когда пулька пробивает брусок:

.

Поделим обе части выражения на m:

.

Выразим соотношение масс из предыдущего выражения:

.

Используем принцип независимости движения тел в поле тяжести по горизонтальной и вертикальной оси и рассмотрим падение бруска и пульки с обрыва.

По вертикальной оси движение обоих тел равноускоренное с ускорением g без начальной скорости.

- время полета каждого тела до падения.

По горизонтальной оси оба тела двигались равномерно с начальными скоростями v₁ и v₂ в течение времени t, которое мы выразили выше. Для бруска: 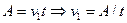. Для пули: .

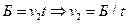Подставим выражения для v₁ и v₂ в формулу для отношения масс, полученную из закона сохранения импульса и получим ответ: .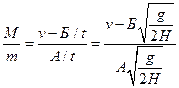

16. Космический зонд разгоняют импульсами нейтральных частиц с массивной платформы, при этом частицы захватываются зондом. Частицы можно выпускать с платформы все сразу или равными долями с интервалом по времени. В конечном итоге масса зонда удваивается. Найти стратегию разгона для достижения наибольшей скорости зонда. Найти эту скорость, если начальная масса зонда m, скорость вылета частиц с платформы V. Гравитационные и релятивистские эффекты не учитывать. Начальная скорость зонда равна нулю.

Решение:

Пусть было решено выпустить N равных долей частиц. Тогда закон сохранения импульса для системы «доля частиц-зонд» после попадания первой доли частиц:

(1) .

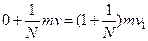После попадания второй доли частиц:

(2) .

…

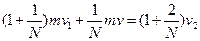После попадания N-той доли частиц импульс зона станет:

(N) .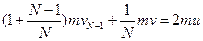

Просуммируем выражения (1)-(N). Члены типа 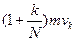в левой и правой части выражения сократятся, и получится 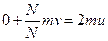. Конечное выражение не зависит от N. Поэтому количество долей частиц не имеет значения.

Конечная скорость зонда: .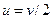

Есть и более короткое решение. Начальный импульс зонда 0. Импульс, который имеют все частицы после выпуска («уносимый импульс»), равен 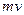. Этот импульс не зависит от стратегии выпуска частиц. После захвата зондом всех частиц его масса удвоится, и импульс зонда станет равным . Запишем закон сохранения импульса с использованием этих данных:

.

Конечная скорость зонда определяется соотношением: 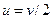, при любой стратегии. Частицы можно выпускать произвольными долями.

Задачи по теме «Колебания. Математический маятник»

17. В совпадающем по направлению гравитационном (g) и электрическом (Е) полях на тонкой нитке длины L подвешено тело массы m и зарядом q. Найти период колебаний тела. Найти период колебаний, если g и Е ортогональны.

Решение:

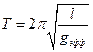Обобщим формулу для расчета периода малых колебаний математического маятника: , где 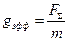- эффективное ускорение свободного падения, сообщаемое равнодействующей всех сил, действующих на данное тело.

а) g и E совпадают по направлению

Пусть сила тяжести и сила электростатического взаимодействия направлены в одну сторону. Тогда, 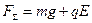. Соответственно, .

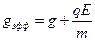Период колебаний маятника будет равен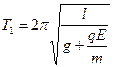

б) g и E ортогональны

Модуль результирующей силы, действующей на заряженный маятник, равен 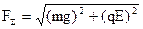. Тогда 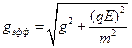. Подставляем в формулу для нахождения периода колебаний: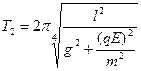

18. Естествоиспытатель изучает колебания маятника (маленький тяжелый шарик на длинной нитке) в движущейся системе отсчета – вагоне поезда. Когда поезд двигался по прямой, период колебаний был Т, когда по закруглению постоянного радиуса – t. Как соотносятся T и t: T>,=,<t? Дорога горизонтальна, скорость поезда постоянна и равна V, радиус закругления R.

Решение:

Формула для расчета периода малых колебаний математического маятника: 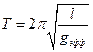, где 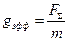- эффективное ускорение свободного падения, сообщаемое равнодействующей всех сил, действующих на данное тело.

Когда поезд едет по прямой и скорость постоянна, на маятник действует только сила тяжести. Период колебаний маятника в этом случае .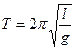

Когда поезд едет по закруглению, в вагоне, как в неинерциальной системе отсчета, возникает центробежная сила: 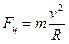. Таким образом, суммарная сила, действующая на маятник, является равнодействующей силы тяжести и центробежной силы:

.

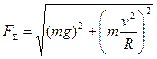Находим 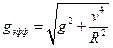. Получаем окончательную формулу для периода колебаний маятника:

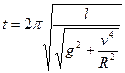. Очевидно, что T>t.

18. Маятник (точечный груз на нерастяжимой нити) приводят в движение, сообщив грузу горизонтальный импульс Р, и он начинает совершать малые колебания с периодом Т. Найти максимальное и минимальное натяжение нити. Масса груза m, поле тяжести g.

Решение:

Максимальное натяжение нити возникает в момент, когда маятник проходит самую нижнюю точку, минимальное, когда маятник отклоняется на максимальный угол от положения равновесия.

Максимальное натяжени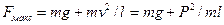е, , где 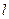- длина маятника.

Минимальное натяжени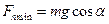е , где 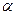- максимальный угол отклонения маятника от положения равновесия.

Период колебания маятника равен

Из закона сохранения энергии можно получить:

Дата добавления: 2015-08-31