Контрольная работа, сентябрь 2006 г

Примеры решения контрольных работ.

Задача 1.

С самолета, летящего горизонтально на высоте Н со скоростью V, сбрасывают мешок с песком. Мешок (масса m) падает в грузовой вагон (масса M) и песок рассыпается по дну вагона. Найти скорость вагона и выделившееся тепло. Вагон первоначально стоял.

Решение:

1) В начальный момент времени мешок обладает только горизонтальной скоростью, равной скорости самолета: .

2) Кинетическая энергия мешка в момент падения на дно вагона определяется из соотношения: = . При попадании мешка в вагон эта энергия мешка будет потрачена на кинетическую энергию вагона с песком и выделившееся тепло :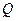

Здесь - горизонтальная скорость вагона с песком (другой у него нет). В соотношении учтено, что .

3) В направлении оси внешние силы не действует (в отличие от оси 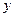, вдоль которой действует сила тяжести), поэтому можно применить закон сохранения горизонтальной компоненты импульса:

,

откуда горизонтальная скорость вагона с песком .

4) С учетом пунктов 3) и 2) получаем: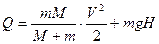

Ответ: скорость вагона , выделившееся тепло .

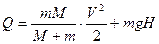Задача 2.

В гравитационном поле g на тонких нитях длины L каждая, закрепленных в одной точке, висят два одинаковых по размеру шара радиуса R<<L и массы m и 2m. Легкий шар отклоняют до горизонтального положения нити и отпускают. Найти, на какие максимальные углы отклонятся шары после первого удара. До удара тяжелый шар покоится. Найти ускорения тел (модуль и направление) сразу же после отпускания легкого тела и сразу же после удара. Найти натяжения нитей в указанные моменты времени. Трения нет, удар абсолютно упругий.

Решение:

1) Пусть 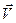- скорость легкого шара до момента удара, - скорость легкого шара после удара, - скорость тяжелого шара после удара.

2) Потенциальная энергия легкого шара переходит в его кинетическую энергию перед столкновением. С учетом выбранной системы координат имеем: , откуда .

3) Кинетическая энергия легкого шара перед ударом переходит в кинетическую энергию легкого и тяжелого шара сразу после удара: или . Кроме этого, суммарный импульс шаров до взаимодействия равен суммарному импульсу после взаимодействия: или 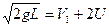. Т.о. имеем систему:

Решая данную систему, получаем: (легкий шар отскакивает от тяжелого в обратную сторону).

4) После взаимодействия кинетическая энергия шаров переходит в потенциальную:

или с учетом 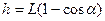и , получаем соотношения:

,

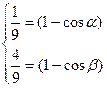откуда , .

5) Сразу после отпускания легкого шара его скорость равна нулю, натяжение нити будет нулевым (см. рисунок до удара), поэтому ускорение будет равно ускорению свободного падения - .

6) Сразу после удара результирующие ускорения буду направлены к точке подвеса и равны: - для легкого шара, - для тяжелого шара. Поскольку длина нити много больше радиусов шаров, то можно считать, что все силы направлены вдоль оси 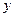. В этом случае, натяжения нитей сразу после удара можно найти из соотношения сил:

или

Ответ: , ; после отпускания легкого шара его ускорение равно ; после удара , , , .

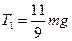Задача 3.

По наклонной плоскости (угол альфа) с постоянной скоростью съезжает доска массы М. Сверху доски находится тело массы m. Тело m удерживается на одном месте нитью, привязанной где-то сверху так, что нить параллельна доске. Найти коэффициент трения между телом m и доской. Между доской и наклонной плоскостью трения нет.

Решение:

1) Силы, действующие на тела, показаны на рисунке. Сила трения действует на тело массы со стороны тела массы 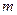и препятствует движению по наклонной плоскости. Сила трения действует на тело массы 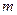со стороны тела массы и под действием этой силы тело 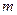могло бы двигаться вдоль плоскости вниз, однако остается на месте, поскольку на него также действует компенсирующая сила натяжения нити .

2) С учетом выбранных осей координат для тела массы 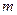можно написать: . По определению , т.е. .

3) На тело действует со стороны тела 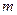сила трения такая же, как на тело массы 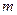со стороны тела массы , т.е. . С учетом того, что тело движется с постоянной скоростью, можно записать: .

4) Итак, с одной стороны , с другой - , откуда

Ответ:

Задача 4.

Из пушки делают два одинаковых выстрела с интервалом 4 секунды. Первый снаряд ударяется в землю через 6 секунд после того, как второй снаряд проходит верхнюю точку траектории. Расстояние от пушки до места падения снарядов 5 километров. Найти минимальное расстояние между снарядами в полете.

Решение:

Рис.1

Рис.2

1) По условию задачи первый снаряд ударяется в землю через 6 с после того, как второй снаряд проходит верхнюю точку траектории. Кроме этого, между выстрелами интервал 4 с (см. рисунок 1). С учетом того, что выстрелы одинаковы, следует, что половина времени в полете равно 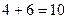с. Полное время полета 20 с.

2) Поскольку полное расстояние равно 5 км, то начальная горизонтальная скорость равна м/с. В дальнейшем эта скорость не меняется.

3) Расстояние между двумя точками определяется из выражения , где - разность координат точек. В случае движения в поле Земли сила тяжести действует только вдоль координаты 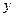. Горизонтальные скорости у снарядов одинаковы, поэтому после второго выстрела и до падения первого снаряда расстояние между ними по горизонтали всегда будет оставаться постоянным и определяться только начальными условиями. Т.о. минимальное расстояние между снарядами будет при условии . Тогда м (см. рисунок 2).

Ответ: Минимальное расстояние между снарядами в полете 1000 м.

Задача 5.

Естествоиспытатель изучает колебания маятника (маленький тяжелый шарик на длинной нитке) в движущейся системе отсчета – вагоне поезда. Когда поезд двигался по прямой, период колебаний был Т, когда по закруглению постоянного радиуса – t. Как соотносятся T и t: T>,=,<t? Дорога горизонтальна, скорость поезда постоянна и равна V, радиус закругления R

Решение:

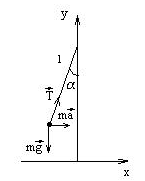
1) В движущемся поезде с постоянной скоростью по прямой период колебания маятника определяется полем тяжести 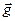и длиной нити : .

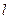2) Если поезд движется по окружности, то на маятник будет находится в поле тяжести 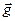и перпендикулярном ему «центробежном» поле , где 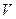- скорость поезда, - радиус поворота железнодорожного полотна. Эффективное поле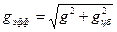

Период колебания, соответственно, будет равен .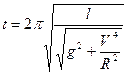

Т.о. .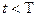

Ответ: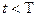

Дата добавления: 2015-08-31