
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Контрольная работа за декабрь 2007 г
|
|
|
|
Задача 1.
В школьном опыте в брусок (масса  кг) стреляют из горизонтально расположенного духового ружья пулькой (масса
кг) стреляют из горизонтально расположенного духового ружья пулькой (масса  г, скорость
г, скорость  м/с). С застрявшей пулькой брусок без вращения смещается по горизонтальной поверхности стола на расстояние
м/с). С застрявшей пулькой брусок без вращения смещается по горизонтальной поверхности стола на расстояние  м. Найти коэффициент трения между столом и бруском
м. Найти коэффициент трения между столом и бруском  .
.
Решение:

1) Пусть скорость пули до влета в брусок  , бруска с пулей
, бруска с пулей  . Из закона сохранения импульса следует,
. Из закона сохранения импульса следует,  , откуда
, откуда  .
.
2) При движении по столу, энергия бруска с пулей идет на совершение работы против силы трения:  . Работа, по определению, равна скалярному произведению силы на перемещение. Сила трения направлена против вектора перемещения
. Работа, по определению, равна скалярному произведению силы на перемещение. Сила трения направлена против вектора перемещения  . Т.о.
. Т.о.  . С учетом 1), получаем
. С учетом 1), получаем
 .
.
Т.е.

Ответ: 
Задача 2.
Из пушки делают два одинаковых выстрела с интервалом 4 секунды. Первый снаряд ударяется в землю через 6 секунд после того, как второй снаряд проходит верхнюю точку траектории. Расстояние от пушки до места падения снарядов 5 километров. Найти минимальное расстояние между снарядами в полете.
Решение: С мотри в разобранных задачах.
Задача 3.
На горизонтальной перекладине на тонких нитях подвешены три шарика с массами m, m1 и m соответственно. Шарики подвешены так, что два крайних соприкасаются со средним, а центры масс всех трех расположены на одной прямой. Левый крайний шарик отклоняют влево, поднимая на высоту h, затем отпускают. На какую максимальную высоту поднимется крайний правый шарик, если а) m1=m б) m1=2m? Все соударения считать абсолютно упругими. Какая из нитей и в какой момент времени будет иметь максимальное натяжение?
Решение:
1)
Пусть 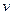 - скорость первого (отклоненного) шарика перед ударом,
- скорость первого (отклоненного) шарика перед ударом,  - скорость первого шарика после взаимодействия со вторым шариком,
- скорость первого шарика после взаимодействия со вторым шариком,  - скорость второго шарика после взаимодействия с первым,
- скорость второго шарика после взаимодействия с первым,  - скорость второго шарика после взаимодействия с третьим,
- скорость второго шарика после взаимодействия с третьим,  - скорость третьего шарика после взаимодействия со вторым.
- скорость третьего шарика после взаимодействия со вторым.
2)
Из закона сохранения для первого шарика имеем: 

 .
.
Считая, что после взаимодействия первый шарик отскакивает в обратную сторону, из закона сохранения импульса можно получить:
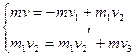
3)
Из закона сохранения энергии имеем:

4)
Т.о. полная система уравнений из четырех неизвестных:
 .
.
Ее решением является:

5)
Для случая  :
:  ,
,  ,
,  ,
, 
6)
Для случая  :
:  ,
, 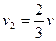 ,
, 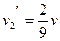 ,
, 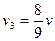
Ответ: а)  ,
,  ,
,  ,
,  , б)
, б)  ,
, 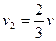 ,
, 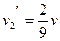 ,
, 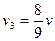
Задача 4.
Как должен двигаться студент ФЕН по горизонтальной поверхности с привязанной на веревочке консервной банкой, чтобы эта банка не ударялась о землю. Длина веревочки L больше высоты студента H. Трения тел о воздух нет. Прим.: задача имеет несколько решений.
Решение: Смотри в разобранных задачах.

Задача 5.
Пружина длины L жесткости k сжата до половины своей длины тонкой ниткой. На концах пружины находятся грузы массами m и M. Нить пережигают. Найти максимальные смещения грузов от своих исходных положений.
Решение:

Система замкнута, поэтому суммарный импульс тел в любой момент времени равен нулю. В частности, в момент остановки одного из тел останавливается и второе. Тогда энергия пружины в момент максимального сжатия равна энергии в момент максимального растяжения:
 , т.е.
, т.е. 
Центр масс также остается на месте, поэтому:

Из приведенных уравнений находим  ,
, 
Ответ:  ,
,  .
.
|
|
|
|
|
Дата добавления: 2015-08-31; Просмотров: 349; Нарушение авторских прав?; Мы поможем в написании вашей работы!