Программа курса лекций 3 страница

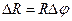
и аналогично

.

Вектор при движении окружности направлен перпендикулярно вектору 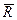, вектор 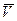направлен вдоль вектора и перпендикулярен вектору 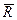, а вектор 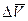перпендикулярен скорости и направлен к центру вращения. Разделив правую и левую часть соотношений на время , в течение которого происходит поворот на угол , для скорости

и центростремительного ускорения

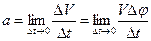
получим:

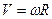
Эквивалентные выражения:

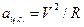
При движении по окружности с постоянной по модулю скоростью тело двигается с постоянным по модулю ускорением, направленным к центру вращения. Соответственно, движение по окружности тела массы осуществляется под действием силы:

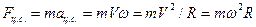
Эта сила направлена к центру вращения, потому ее называют центростремительной силой. Роль центростремительной силы может выполнять сила трения при движении автомобиля на повороте дороги, сила натяжения веревки при вращении привязанного тела, например камня, сила тяжести.

Спутник на орбите.

Примером движения тела под действием центростремительной силы является движение космического корабля по круговой орбите вокруг Земли. В этом случае роль центростремительной силы выполняет сила притяжения корабля к Земле. По второму закону Ньютона:

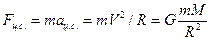
Вблизи Земли

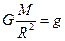
В соответствии с этим первая космическая скорость

.

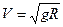Подставляя значения , радиус Земли 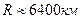, получим .

Колесо на дороге. Твердое тело.

Если колесо радиуса 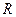(например, колесо велосипеда) вращается относительно неподвижной оси (велосипед неподвижен, колесо приподнято) с постоянной угловой скоростью 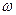, то каждая точка обода колеса имеет относительно оси некоторую скорость 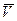, направленную по касательной к окружности обода колеса, при этом , и ускорение , направленное к оси.

Пусть велосипед движется «относительно» горизонтальной дороги с постоянной скоростью 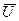. Тогда, в соответствии с правилом сложения скоростей, в лабораторной системе «дорога» каждая точка обода колеса движется со скоростью

Если колесо не проскальзывает относительно дороги, то скорость точки колеса, соприкасающейся с дорогой в данный момент времени, относительно дороги равна нулю:

, .

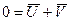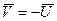В соответствии с этим, скорость точек обода колеса относительно оси по модулю равна скорости колеса относительно дороги:

Поскольку велосипед движется с постоянной скоростью, в данном случае переход из системы отсчета «дорога» в систему отсчета «велосипед» - это переход из одной инерциальной системы отсчета в другую инерциальную систему отсчета. В соответствии с преобразованиями Галилея в той и другой системе отсчета все точки обода колеса имеют одинаковое ускорение

,

направленное к оси колеса.

Задача. Для точек катящегося колеса нарисовать вектора скоростей и ускорений.

Рассмотрим кинетическую энергию колеса, катящегося по дороге.

Будем считать, ось колеса направлена вдоль оси X, само колесо находится и остается при движении в плоскости ZY.

Пусть в лабораторной системе отсчета XYZ «дорога»

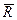- радиус вектор центра (оси) колеса,

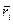- радиус вектор элемента обода колеса с массой в лабораторной системе отсчета XYZ, и

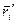- радиус-вектор этого элемента колеса относительно оси вращения, т.е. в движущейся системе отсчета. Выполняются векторные соотношения:

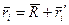
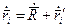
Кинетическая энергия катящегося по дороге колеса равна сумме кинетических энергий его элементов . В системе отсчета «дорога»:

Рассмотрим отдельные части полученной суммы.

Поскольку

,

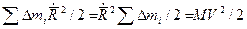первая часть суммы - кинетическая энергия поступательного движения колеса как целого тела массы , имеющего скорость .

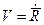Кинетическая энергия вращения - вторая часть суммы:

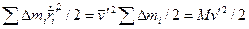
Такую энергию имеет приподнятое вращающееся колесо стоящего велосипеда. Скорость всех точек обода колеса относительно неподвижной оси колеса одинакова и равна .

Третья часть суммы

.

Величина

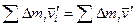
является импульсом колеса в системе отсчета, связанной с его осью. Относительно оси импульс колеса равен нулю, что следует из «соображений симметрии».

Если нет проскальзывания, то 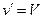, и для колеса, вся масса которого сосредоточена в ободе, полная кинетическая энергия

Колесо является частным случаем твердого тела. Кинетическая энергия колеса в частности и твердого тела в общем случае складывается из кинетической энергии поступательного движения тела как целого, и кинетической энергии вращения – энергии движения элементов тела относительно неподвижной оси вращения, проходящей через центр инерции.

Выражение для кинетической энергии вращения может быть преобразовано. При вращении колеса относительно неподвижной оси все его точки вращаются с одинаковой угловой скоростью 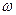. Для каждой точки массы , находящейся от оси вращения на расстоянии 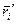, выполняются соотношение: . Тогда кинетическая энергия вращения

Моментом инерции твердого тела относительно оси вращения называется величина

Момент инерции при вращении твердого тела играет такую же роль, какую играет масса при поступательном движении материальной точки.

Для колеса радиуса 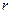, вся масса 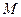которого сосредоточена в ободе, момент инерции относительно оси

В общем случае твердое тело имеет три главных момента инерции относительно трех взаимно перпендикулярных осей – главных осей инерции. Главные оси инерции проходят через центр инерции тела.

Твердое тело, у которого все три главных момента инерции относительно главных осей инерции различны, называется асимметричным волчком. При свободном вращении такое тело может одновременно вращаться относительно главных осей инерции с тремя различными угловыми скоростями.

Если , такое тело называется симметричным волчком. При свободном вращении такое тело равномерно вращается относительно оси симметрии и одновременно эта ось совершает регулярную прецессию (с постоянной угловой скоростью) относительно направления сохраняющегося момента импульса тела.

Пример – плоский однородный диск, колесо велосипеда, однородный цилиндр.

Если , такое тело называется шаровым волчком.

Свободное вращение такого тела происходит с постоянной угловой скоростью относительно постоянной оси.

Если , , 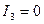такое тело называется ротатором.

Свободное вращение ротатора – вращение с постоянной угловой скоростью в одной плоскости вокруг направления, перпендикулярного к этой плоскости.

Пример – две частицы, закрепленные на невесомом стержне, тонкая спица.

10. Неинерциальные системы отсчета

Принцип эквивалентности: поле тяготения в небольшой области пространства и времени (в которой его можно считать однородным и постоянным во времени) по своему проявлению тождественно ускоряющейся системе отсчета.

Эквивалентное поле: фиктивное (воображаемое) поле тяготения, действующее в ускоряющейся системе отсчета. Сложение реального и фиктивного полей. «Антигравитация».

Разбор задач.

Ракета. Лифт. Воздушный шарик в лифте, ракете. Свечка и отвес в ускоряющейся электричке. Свечка во вращающейся комнате. Космический корабль на стационарной орбите. Форма жидкости во вращающемся стакане. Жидкость в аквариуме, спускающемся по наклонной плоскости. Закон Архимеда в неинерциальной (ускоряющейся) системе отсчета. Малые колебания в неинерциальной системе отсчета.

11. Механика в целом.

Метод Галилея. Функция. Роль моделей в механике, науке и жизни. Аксиоматический подход к построению моделей мира. Законы механики Галилея-Ньютона – физико-математическая модель мира. Относительность моделей и абсолютность суждений в рамках моделей. Теория против эксперимента. Законы сохранения. Современная «Стандартная модель».

Рекомендованная литература к теоретическому курсу

1. Физический энциклопедический словарь. М.: «Советская энциклопедия», 1983.

2. Физика. Учебное пособие для 10 класса школ и классов с углубленным изучением физики. Под редакцией А.А. Пинского. М.: «Просвещение», 1995.

3. Физика. Учебник для 9 класса средней школы. А.П.Ершов, И.И.Воробъев. В.Г.Харитонов. Под редакцией Е.И.Биченкова. Новосибирск: Издательльство НГУ, 1997.

4. И.В. Савельев. Курс физики. Т. I. Механика. Молекулярная физика. M.: Наука, 1989.

5. Л.Д.Ландау и Е.М.Лифшиц. Механика. М.: ГИФМЛ, 1958.

Дата добавления: 2015-08-31