Экзаменационный билет № 6

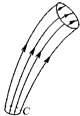
Линией тока называется касательная, которая указывает направление скорости молекулы жидкости в настоящий момент времени. Молекула в этот момент должна находиться в точке касания. Некоторая трубчатая поверхность, образованная линиями тока, проходящими через произвольный замкнутый контур, называется трубкой тока. Рассмотрим трубку тока с бесконечно малым сечением 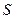. В ней скорость жидкости одинакова во всех точках одного и того же поперечного сечения и направлена вдоль оси трубки тока. ­– масса жидкости протекающей за время через поперечное сечение трубки. Если течение стационарное, то 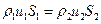. Если жидкость несжимаема, т.е. 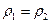, то 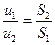– уравнение неразрывности.

Идеальная жидкость – пренебрегаем силами вязкости; нет касательных и касательных и нормальных сил внутреннего трения при движении; единственная поверхностная сила, действующая на жидкость – сила нормального давления , однозначно определяемая плотностью и температурой жидкости; жидкость считается несжимаемой.

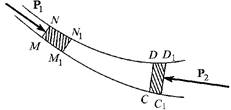
Рассмотрим стационарное движение идеальной жидкости в поле силы тяжести. Пренебрегая теплообменом, применяем закон сохранения жидкости. Для этого необходимо выделить в жидкости узкую трубку тока с бесконечно малым диаметром поперечного сечения и рассмотреть объем 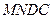. Пусть объем жидкости переместился на бесконечно близкое положение 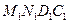. Вычислим работу , совершаемую силами давления. Работа по перемещению границы 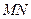в – , где – величина перемещения. 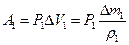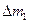, тогда , где – масса жидкости в объеме . 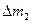Для объема произведем те же расчеты и получим , где – масса жидкости в объеме . Т.к. движение жидкости стационарно, то .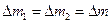

Работа совершенная внешним давлением .

Эта работа ровна приращению 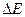полной энергии выделенной части жидкости. Энергия в объеме не и изменилась, т.к. движение стационарно. Значит 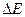– разность энергий массы жидкости 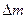в положениях и . – полная энергия, которая приходится на единицу массы данной жидкости. Отсюда . Приравниваем к работе и получаем .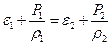

Можно сделать вывод, что вдоль одной и той же линии тока, если течение идеальной жидкости стационарно, величина постоянна: ­– уравнение Бернулли.

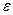складывается из потенциальной и кинетической энергии – . Учитывая это мы, можем переписать уравнение Бернулли в таком виде .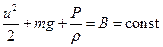

Если вертикальный цилиндрический сосуд наполненный жидкостью равномерно вращать вокруг своей оси, то жидкость также приходит во вращение. Сначала начинают двигаться слои, находящиеся ближе к вертикальной поверхности сосуда. Затем вращение передается внутренним слоям. Вскоре жидкость начнет вращаться равномерно, как твердое тело. Это говорит о том, что существуют некие касательные силы между сосудом и жидкостью, а так же между слоями жидкости. Эти касательные силы называются силами трения – внутренними (между слоями жидкости) и внешними (между жидкостью и стенкой сосуда). Силы внутреннего трения – силы вязкости.

Рассмотрим две параллельные бесконечно длинные пластинки, между которыми находится слой жидкости. Пусть одна из пластинок движется с постоянной скоростью относительно другой. Необходимо все время прикладывать к движущейся пластинке силу 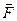для того, чтобы пластинка двигалась равномерно. Для того, чтобы вторая пластинка находилась в состоянии покоя, на нее должна действовать точно такая же сила, направленная в противоположную сторону 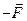. Модуль этой силы был установлен экспериментально:

,

где 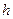– расстояние между пластинками; 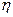– постоянная, называемая вязкостью жидкости. 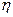зависит от материала пластинок и имеет различные значения для различных жидкостей. Для конкретной жидкости 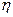зависит от различных параметров, характеризующих ее внутреннее состояние (в первую очередь от температуры).

Вязкая несжимаемая жидкость течет вдоль прямолинейной цилиндрической трубы радиусом 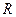. Т.к. жидкость несжимаемая, она не меняет скорости тока вдоль трубы. Но она меняется в зависимости от 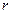, т.е. 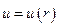. Выделим в трубе бесконечно короткую цилиндрическую часть с радиусом 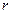и длиной . На ее боковую поверхность действует касательная сила вязкости . На

основание цилиндра действует сила разности давлений 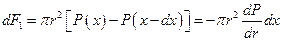. Если движение стационарно, то сумма этих сил должна быть равна нулю, значит можно записать 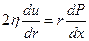. Т.к. и вместе с ней не зависят от , то и должна быть постоянна и равняться , где – давление на входе трубы, 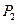– давление на выходе трубы, 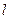– длина трубы. Учитывая все вышеприведенное получаем 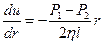. После интегрирования 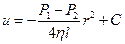. 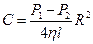, из условия, что при скорость движения жидкости равна нулю. В итоге получили 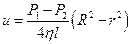. Из этого уравнения видно, что скорость максимальна на оси трубы. Там она достигает значения .

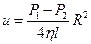Найдем какой расход жидкости протекающей через сечение трубы. Масса жидкости проходящей каждую секунду через кольцевую площадку с внутренним радиусом 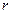и внешним 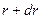будет равна 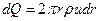. Подставляем выражение для скорости и интегрируем . Найдя интеграл, увидим, что –

Дата добавления: 2015-08-31