Экзаменационный билет № 7

Упругая деформация — деформация, исчезающая после прекращения действий на тело внешних сил. При этом тело принимает первоначальные размеры и форму.

Область физики, изучающая упругие деформации, называется теорией упругости.

При упругой деформации её величина не зависит от предыстории и полностью определяется механическими напряжениями, то есть является однозначной функцией от напряжений. Для большинства веществ эту зависимость можно с хорошей точностью считать прямой пропорциональностью. При этом упругая деформация описывается законом Гука. Наибольшее напряжение, при котором закон Гука справедлив, называется пределом пропорциональности.

Некоторые вещества (металлы, каучуки) могут претерпевать значительную упругую деформацию, в то время как у других (керамики, прессованные материалы) даже ничтожная деформация перестаёт быть упругой.

Максимальное механическое напряжение, при котором деформация ещё остаётся упругой, называется пределом текучести. Выше этого предела деформация становится пластической.

Упругие деформации могут изменяться периодически со временем (упругие колебания). Процесс распространения упругих колебаний в среде называют упругими волнами.

Коэффициент Пуассона (обозначается как или 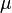) — величина отношения относительного поперечного сжатия к относительному продольному растяжению. Этот коэффициент зависит не от размеров тела, а от природы материала, из которого изготовлен образец. Коэффициент Пуассона и модуль Юнга полностью характеризуют упругие свойства изотропного материала. Безразмерен, но может быть указан в относительных единицах: мм/мм, м/м.

Описание[править | править вики-текст]

При приложении к телу растягивающего усилия оно начинает удлиняться в продольном направлении, а поперечное сечение уменьшается. Коэффициент Пуассона показывает во сколько раз относительное уменьшение поперечного размера деформируемого тела больше относительного увеличения его длины при растяжении. Для абсолютно хрупкого материала коэффициент Пуассона равен 0, для абсолютно несжимаемого — 0,5. Для большинства сталей этот коэффициент лежит в районе 0,3, для резины он примерно равен 0,5.

Ауксетики[править | править вики-текст]

Основная статья: Ауксетики

Существуют также материалы (преимущественно полимеры), у которых коэффициент Пуассона отрицателен, такие материалы называют ауксетиками. Это значит, что при приложении растягивающего усилия поперечное сечение тела увеличивается.

К примеру, бумага из одно слойных нанотрубок имеет положительный коэффициент Пуассона, а по мере увеличения доли много слойных нанотрубок наблюдается резкий переход к отрицательному значению −0,20.

Отрицательным коэффициентом Пуассона обладают многие анизотропные кристаллы^[1], так как коэффициент Пуассона для таких материалов зависит от угла ориентации кристаллической структуры относительно оси растяжения. Отрицательный коэффициент обнаруживается у таких материалов, как литий (минимальное значение равно −0.54), натрий (−0.44), калий (−0.42), кальций (−0.27), медь (−0.13) и других. 67 % кубических кристаллов из таблицы Менделеева имеют отрицательный коэффициент Пуассона.

Уравнение[править | править вики-текст]

,

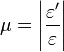где

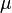— коэффициент Пуассона;

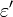— деформация в поперечном направлении (отрицательна при осевом растяжении, положительна при осевом сжатии);

— продольная деформация (положительна при осевом растяжении, отрицательна при осевом сжатии).

Модуль Юнга (модуль продольной упругости) — физическая величина, характеризующая свойства материала сопротивляться растяжению/сжатию при упругой деформации^[1]. Назван в честь английского физика XIX века Томаса Юнга. В динамических задачах механики модуль Юнга рассматривается в более общем смысле — как функционал среды и процесса. В Международной системе единиц (СИ) измеряется в ньютонах на метр в квадрате или в паскалях. Является одним из модулей упругости.

Модуль Юнга рассчитывается следующим образом:

где:

• F — нормальная составляющая силы,
• S — площадь поверхности, по которой распределено действие силы,
• l — длина деформируемого стержня,
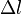• — модуль изменения длины стержня в результате упругой деформации (измеренного в тех же единицах, что и длина l).

Через модуль Юнга вычисляется скорость распространения продольной волны в тонком стержне:

где — плотность вещества.

Энергию деформированного упругого тела также называют энергией положения или потенциальной энергией (ее называют чаще упругой энергией), так как она зависит от взаимного положения частей тела, например витков пружины. Работа, которую может совершить растянутая пружина при перемещении ее конца, зависит только от начального и конечного растяжений пружины. Найдем работу, которую может совершить растянутая пружина, возвращаясь к нерастянутому состоянию, т.е. найдем упругую энергию растянутой пружины.

Пусть, например, растянутая пружина закреплена одним концом, а второй конец, перемещаясь, совершает работу. При нахождении работы мы должны учитывать, что сила, с которой действует пружина, не остается постоянной при изменении растяжения. Мы видели (§ 37), что сила упругости пружины пропорциональна ее растяжению. Если первоначальное растяжение пружины, считая от ее нерастянутого состояния, равнялось l, то первоначальное значение силы упругости составляло F=kl, где k — коэффициент пропорциональности, который называют коэффициентом упругости пружины. По мере сокращения пружины эта сила равномерно убывает от значения kl до нуля.

Значит, среднее значение силы равно F_ср=kl. Можно показать, что для вычисления работы А изменяющейся силы упругости нужно это среднее значение силы умножить на перемещение точки приложения силы:

A=1/2 kl•l=1/2kl².

Таким образом, потенциальная энергия упругости Е_п равна

E_п = 1/2 kl². (98.1)

Здесь потенциальная энергия выражена через коэффициент упругости пружины и через наибольшее растяжение ее. Полученное выражение для потенциальной энергии можно записать и иначе, через величину силы упругости при наибольшем растяжении и коэффициент упругости:

(98.2)

Из этой формулы видно, что, растягивая с одной и той же силой разные пружины, мы сообщим им различный запас потенциальной энергии: чем жестче пружина, т. е. чем больше коэффициент упругости, тем меньше потенциальная энергия; и наоборот: чем мягче пружина, тем больше энергия, которую она запасет при данной силе, растянувшей ее. Это можно уяснить себе наглядно, если учесть, что при одинаковых действующих силах растяжение мягкой пружины больше, чем жесткой, а потому больше и произведение силы на путь точки приложения силы, т. е. работа.

Это имеет большое значение, например, при устройстве различных рессор и амортизаторов: при посадке на землю самолета амортизатор шасси, сжимаясь, должен произвести большую работу, погашая вертикальную скорость самолета. В амортизаторе с малой жесткостью сжатие будет больше, зато возникающие силы будут меньше и конструкция самолета будет лучше предохранена от повреждений. По той же причине при тугой накачке шин велосипеда дорожные толчки ощущаются резче, чем при слабой накачке.

В классической статистической физике распределение частиц не зависит от квантовомеханических характеристик частиц. Вместе с тем в квантовой механике показывается, что ансамбли, состоящие из нескольких тождественных частиц, описываются либо симметричными, либо антисимметричными относительно перестановок частиц волновыми функциями. Вид волновых функций зависит от значения собственного механического момента – спина частиц, из которых состоят ансамбли. Если спин частиц целый (в единицах ), то такие ансамбли описываются симметричными волновыми функциями. Частицы, имеющие целое значение спина, получили название Бозе-частицы, или бозоны. К ним относятся, в частности, K- и -мезоны (спин 0), фотоны (спин 1), атомы, у которых суммарный спин электронов, протонов и нейтронов, входящих в состав атома, оказывается целым, например 4 2He. Частицы, имеющие полуцелое значение спина, описываются антисимметричными волновыми функциями и получили название Ферми-частицы, или фермионы. К ним относятся, в частности, электрон, протон, нейтрон и их анти

Дата добавления: 2015-08-31