Магнитное поле постоянных токов в вакууме. Основные уравнения магнитостатики в вакууме. Закон Био-Савара. Сила Ампера. Сила Лоренца

Мы бы никогда не знали о магнитном поле, если бы оно себя не проявляло. Определить наличие поля можно стрелкой компаса. Стрелка компаса будет только сигнализатором наличия поля. Для получения количественных величин стрелка непригодна. В качестве измерителя поля можно использовать вращающуюся рамку.

Амплитуда напряжения на токосъемных кольцах равна

Где:

N – число витков в рамке;

Ф – магнитный поток Вб;

ω – угловая частота вращения равная 2π f

По замеренному напряжению можно рассчитать магнитный поток, измеряемый в веберах (Вб). Магнитный поток и есть величина, характеризующая поле. Зная магнитный поток, можно рассчитать напряжение, которое мы можем получить в генераторе. На практике чаще пользуются понятием плотности магнитного потока, т.е. потоком, проходящим сквозь площадку площадью 1 квадратный метр. Плотность магнитного потока называется магнитной индукцией.

B = Ф/ S

Магнитная индукция измеряется в теслах (Тл).

Причиной возникновения магнитного потока является электрический ток. Магнитная индукция на расстоянии r от прямолинейного проводника равна:

По центру витка с током радиуса r магнитная индукция будет равна

Этой характеристикой магнитного потока – индукцией и можно было бы ограничиться при изучении магнетизма. Но традиционно преподается, что электрический ток порождает напряженность магнитного поля, а уж та в свою очередь порождает индукцию.

Это напоминает индийский уклад офиса. В Индии начальник, чтобы включить вентилятор вызывает секретаршу. Та говорит: «Хорошо», - кланяется и уходит; через полчаса приходит электрик и, наконец, вентилятор начинает вращаться..

Напряженность магнитного поля измеряется в А/м.

Для прямолинейного провода с током

Для витка с током напряженность в центре витка равна

Это те же самые формулы, которые приведены выше для индукции. Различаются они лишь магнитной постоянной μ₀.

Индукция в вакууме или воздухе равна

Где:

μ₀ - магнитная постоянная, равная 4π·10^-7

То есть, индукция и напряженность различаются только масштабом единиц. И одно из этих понятий для наших сугубо практических целей излишне. И можно было бы все формулы и графики пересчитать на B, но читателям этой статьи придется пользоваться специальной литературой, где H наличествует, поэтому я оставлю по большинству традиционный стиль формул.

Основные уравнения[править | править вики-текст]

Все основные уравнения магнитостатики линейны^[1] (как и классической электродинамики вообще, частным случаем которой магнитостатика является). Это подразумевает важную роль в магнитостатике (тоже как и во всей электродинамике) принципа суперпозиции.

· Принцип суперпозиции для магнитостатики может быть сформулирован так: Магнитное поле, создаваемое несколькими токами, есть векторная сумма полей, которые бы создавались каждым из этих токов по отдельности.

Этот принцип одинаково формулируется и в принципе одинаково используется для вектора магнитной индукции и для векторного потенциала и применяется при расчетах повсеместно. Особенно очевидным и прямым образом это проявляется, когда при применении закона Био — Савара (см. ниже) для расчета магнитного поля производится суммирование (интегрирование) бесконечно малых вкладов , создаваемых каждым бесконечно малым элементом тока, текущих в разных точках пространства (точно так же и при применении варианта этого закона для векторного потенциала).

Основные уравнения, используемые в магнитостатике^[2]:

· Закон Био — Савара — Лапласа (величина магнитного поля, генерируемого в данной точке элементом тока)

· Теорема о циркуляции магнитного поля

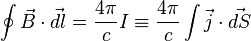
· она же в дифференциальной форме:

· Выражение для силы Лоренца (силы, с которой на движущуюся заряженную частицу действует магнитное поле)

· Выражение для силы Ампера (силы, с которой на элемент тока действует магнитное поле)

(уравнения выше записаны в гауссовой системе единиц); в других системах единиц эти формулы отличаются только постоянными коэффициентами, например:

в системе СИ [показать]

Здесь — вектор магнитной индукции, I — сила тока в проводнике (а в теореме о циркуляции — суммарный ток через поверхность), — элемент проводника (в теореме о циркуляции — элемент контура интегрирования), — радиус-вектор, проведённый из элемента тока в точку, в которой определяется магнитное поле, — плотность тока, — величина заряда и скорость заряженной частицы.

· Для расчёта магнитного поля в магнитостатике можно пользоваться (и часто это весьма удобно) понятием магнитного заряда, делающим аналогию магнитостатики с электростатикой более детальной и позволяющим применять в магнитостатике формулы, аналогичные формулам электростатики — но не для электрического, а для магнитного поля. Обычно (за исключением случая теоретического рассмотрения гипотетических магнитных монополей) подразумевается лишь чисто формальное использование, так как в реальности магнитные заряды не обнаружены. Такое формальное использование (фиктивных) магнитных зарядов возможно благодаря теореме эквивалентности поля магнитных зарядов и поля постоянных электрических токов. Фиктивные магнитные заряды можно использовать при решении разных задач как в качестве источников магнитного поля (например, магнитом или катушкой), так и для определения действия внешних магнитных полей на магнитное тело (магнит, катушку).

Закон Био — Савара — Лапласа. Если известно выражение, определяющее вектор индукции магнитного поля, создаваемого одним движущимся электрическим зарядом (4.11), то задача нахождения индукциимагнитного поля, создаваемого электрическим током в проводнике любой формы, должна быть в принципе разрешимой. Для решения такой задачи необходимо определить индукцию магнитного поля, созданного в данной точке первым зарядом участвующим в создании электрического тока в проводнике, затем индукцию магнитного поля,

Рис. 85. Индукция магнитного поля движущегося электрического заряда в данной точке зависит от расстояния до этой точки и направления вектора скорости

Рис. 86. Индукцию магнитного поля проводника с током можно найти как сумму векторов индукции отдельных зарядов, создающих электрический ток

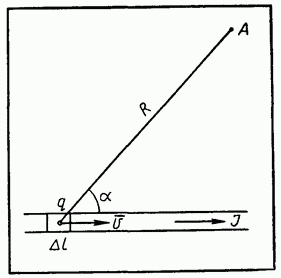
Рис. 87. Элемент проводника с током можно рассматривать как движущийся электрический заряд

созданного в той же точке зарядом и т. д. для всех остальных электрических зарядов до последнего Векториндукции магнитного поля тока в данной точке А может быть найден как геометрическая сумма векторовмагнитной индукции всех электрических зарядов, участвующих в создании электрического тока в проводнике (рис. 86):

Разумеется, расчеты никогда не выполняются буквально таким способом. Решение задачи о нахождениииндукции магнитного поля проводника с током можно упростить следующим образом.

Рассмотрим прямолинейный элемент проводника длиной в котором протекает электрический ток (рис. 87). Так как за малый интервал времени свободные заряды в проводнике, движущиеся со скоростью упорядоченного движения переместятся на расстояние а количество заряда, протекшего за то же время через поперечное сечение проводника, равно: то количество свободных зарядов в элементе проводника длиной равно:

Если длина прямолинейного элемента проводника мала по сравнению с расстоянием от него до точки, в которой определяется индукция магнитного поля тока, протекающий в нем ток можно рассматривать какэлектрический заряд движущийся со скоростью . Индукция магнитного поля от этого элемента проводника с током

согласно выражениям (4.11) и (4.12) в точке А на расстоянии R от элемента проводника в направлении под углом к нему равна:

Это выражение было найдено Лапласом на основании анализа результатов, полученных Био и Саваром при экспериментальном исследовании магнитных полей с током и носит название закона Био — Савара — Лапласа.

Магнитная индукция кругового тока и бесконечного прямого тока. Используя закон Био — Савара—Лапласа, можно вычислить индукцию магнитного поля, создаваемого при прохождении тока через проводники любых размеров и форм. В практикуме по решению задач к этой главе найдено выражение, с помощью которого можно вычислить индукцию магнитного поля, создаваемого круговым током радиусом R в центре круга (задача 42):

Индукция магнитного поля на расстоянии от бесконечного прямого проводника с током определяется выражением:

Зако́нАмпе́ра — закон взаимодействия электрических токов. Впервые был установлен Андре Мари Ампером в 1820 для постоянного тока. Из закона Ампера следует, что параллельные проводники с электрическими токами, текущими в одном направлении, притягиваются, а в противоположных — отталкиваются. Законом Ампера называется также закон, определяющий силу, с которой магнитное поле действует на малый отрезок проводника с током. Выражение для силы , с которой магнитное поле действует на элемент объёма 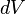проводника с током плотности , находящегося в магнитном поле с индукцией , в Международной системе единиц (СИ) имеет вид:

.

Если ток течёт по тонкому проводнику, то , где — «элемент длины» проводника — вектор, по модулю равный и совпадающий по направлению с током. Тогда предыдущее равенство можно переписать следующим образом:

Сила , с которой магнитное поле действует на элемент проводника с током, находящегося в магнитном поле, прямо пропорциональна силе тока 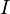в проводнике и векторному произведению элемента длины проводника на магнитную индукцию :

Направление силы определяется по правилу вычисления векторного произведения, которое удобно запомнить при помощиправила левой руки.

Модуль силы Ампера можно найти по формуле:

где — угол между векторами магнитной индукции и тока.

Сила максимальна когда элемент проводника с током расположен перпендикулярно линиям магнитной индукции ():

Сила Лоренца — сила, с которой электромагнитное поле согласно классической (неквантовой) электродинамике действует наточечную заряженную частицу. Иногда силой Лоренца называют силу, действующую на движущийся со скоростью заряд лишь со стороны магнитного поля, нередко же полную силу — со стороны электромагнитного поля вообще^[1], иначе говоря, со стороныэлектрического 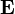и магнитного полей. В Международной системе единиц (СИ) выражается как:

Названа в честь голландского физика Хендрика Лоренца, который вывел выражение для этой силы в 1892 году. За три года до Лоренца правильное выражение было найдено О. Хевисайдом^[2].

Макроскопическим проявлением силы Лоренца является сила Ампера.

Для силы Лоренца, так же как и для сил инерции, третий закон Ньютона не выполняется. Лишь переформулировав этот закон Ньютона как закон сохранения импульса в замкнутой системе из частиц и электромагнитного поля, можно восстановить его справедливость для сил Лоренца^[

16.2 Квантовая природа света. Внешний фотоэффект. Уравнение Эйнштейна. Эффект Комптона.
Классические представления о волновой природе электромагнитного излучения позволили успешно объяснить явления интерференции, дифракции и поляризации и создать высокоточную теорию оптических приборов. Однако исследование процессов взаимодействия электромагнитных волн с веществом выявило ограниченность области применимости этих представлений. С точки зрения классической теории ускоренно движущийся заряд излучает или поглощает электромагнитные волны, интенсивность которых пропорциональна квадрату ускорения. Для непериодического движения интенсивность волны отлична от нуля в широком интервале частот. Такой спектр излучения называется сплошным. Если движения частицы является гармоническим с частотой w, то излучаемая волна имеет ту же частоту. Спектр излучения, содержащий дискретный набор частот, называется линейчатым или дискретными.

^ Проблема устойчивости атомов. Опытами Резерфорда было установлено, что в целом нейтральный атом состоит из малого в сравнении с ним положительного ядра, в котором сосредоточена почти вся масса (>99%) и электронов. Согласно теореме Ирншоу (см. лекцию № 3 в [3]) эта система не может быть устойчивой, находясь в покое. Поэтому Резерфорд пришел к так называемой планетарной модели атома, в которой электроны вращаются вокруг ядра подобно планетам солнечной системы. По законам классической электродинамики такие электроны должны непрерывно излучать, поскольку под действием притяжения ядра испытывают ускорение. В результате электроны должны быстро (за время ~10^-11 с) упасть на ядро. Таким образом, и при наличии движения в рамках классической физики модель взаимодействующих по закону Кулона зарядов оказывается неустойчивой.

Устойчивость классическому атому могут придать некулоновские силы. Но и они не спасают положение. В этом случае не удается объяснить атомные спектры. При любых силах спектр классического излучения должен либо быть непрерывным, либо состоять из основных частот и кратных им гармоник. На самом деле кратных частот в дискретных спектрах атомов не наблюдается. Таким образом, устойчивость атомов и характер их спектров не могут быть объяснены в рамках классической физики.

Фотоэффект. Явное несоответствие выводов, следующих из классической теории, с экспериментальными данными обнаружилось при изучении фотоэффекта. Вырывание электронов с поверхности металлов под действием электромаг­нитной волны называется внешним фотоэффектом. При внутреннем фото­эффекте в объеме вещества увеличивается концентрация свободных электронов, в результате чего увеличивается его электропроводность. Схема установки по исследованию внешнего фотоэффекта (в дальнейшем - фотоэффекта) приведена на рис. 1.1. Катод К облучается электромагнитными волнами видимого или ультрафиолетового диапазона. Амперметр А измеряет ток, протекающий между катодом и анодом Ан (фототок). Батарея источников Э.Д.С. e и переменное сопротивление R позволяют изменять как величину, так и знак напряжения U между катодом и анодом, измеряемого вольтметром V. Изменяя подключение батареи можно изменять также и знак напряжения.

В ольт-амперная характеристика фотоэффекта приведена на рис. 1.2. Здесь положительным считается напряжение, при котором катод заряжен отрицательно. С ростом U с фототок растет и достигает своего максимального значения I_Н, называемого током насыщения в том случае, если все выбитые с катода заряды достигают анода. Знак U свидетельствует о том, что поверхность катода покидают отрицательные заряды – электроны. Модуль отрицательного напряжения U_З, при котором фототок прекращается, называется задерживающим напряжением.

Рис. 1.1

Величина U_З позволяетопределить энергию eU_З, которой обладает фотоэлектрон. Систематические исследования, выполненные профессором Московского университета А.Г. Столетовым, позволили сформулировать следующие законы фотоэффекта:

1.
Фототок пропорционален интенсивности излучения.

2.
Существует длина волны l_КР (красная или более точно длинноволновая граница фотоэффекта), разграничивающая области излучения, способного (l<l_КР) и неспособного (l>l_КР) вызывать фотоэффект. Величина l_КР зависит от материала катода и не зависит от интенсивности излучения.

3.

Рис. 1.2

4.
Энергия фотоэлектрона E линейно зависит от частоты волны и не зависит от интенсивности излучения.

5.
Фототок возникает практически мгновенно после начала облучения катода. На этом свойстве - безинерционости фотоэффекта основаны многие его практические применения.

По классическим представлениям энергия волны, а следовательно и энергия поглощаемая частицей, пропорциональна интенсивности падающего излучения. Поэтому с классической точки зрения наличие красной границы при любой интенсивности и независимость энергии фотоэлектрона от интенсивности не могут быть объяснены. Время накопление энергии частицей в классической физике определяется мощностью источника. В стандартных условиях эксперимента электрон может поглотить непрерывно распространяющуюся энергию, достаточную для отрыва от металла, за время, превышающее 1 с, что противоречит безинерционости фотоэффекта.

^ Фотон. Уравнение Эйнштейна. Для объяснения фотоэффекта Эйнштейн (1905 г.) ввел понятие фотонов, согласно которому излучение переносится квантами (частицами), летящими со скоростью света. Энергия фотонов E _Ф пропорциональна частоте излучения n

. (1.1)

Коэффициент пропорциональности h = 6,62·10^-34 Дж ·с называется постоянной Планка. Согласно специальной теории относительности энергия такой частицы с нулевой массой покоя и движущейся со скоростью света следующим образом связана с ее импульсом

. (1.2)

Следовательно, импульс фотона

, (1.3)

где – длина волны света.

Фотон, попадая в металл, отдает свою энергию одному электрону и таким образом выбивает его из металла. При вылете электрон теряет часть энергии A, равную работе, необходимой для его освобождения (работе выхода). Закон сохранения энергии в этом случае имеет вид

. (1.4)

Уравнение (1.4), называемое уравнением Эйнштейна, полностью объясняет законы фотоэффекта.

1.
Число выбитых электронов пропорционально числу падающих квантов, а, следовательно, и интенсивности света.

2.
Если энергия фотона меньше работы выхода, энергия фотоэлектрона оста­ется отрицательной, что объясняет наличие красной границы.

3.
Из уравнения Эйнштейна непосредственно следует линейная зависимость энергии фотоэлектрона E от частоты волны.

4.
Квант энергии поглощается электроном практически мгновенно, что объясняет безинерционость фотоэффекта.

Источники интенсивного излучения (лазеры) позволяют наблюдать маловероятные в обычных условиях процессы одновременного поглощения N> 1 фотонов – многофотонный фотоэффект. В экспериментах N может достигать значений ~10². Уравнение Эйнштейна в этом случае имеет вид

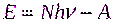. (1.5)

^ Эффект Комптона. Явление фотоэффекта доказывает тот факт, что энергетический обмен между светом и веществом носит квантовый характер. Корпускулярная природа света наиболее наглядно проявляется при взаимодей­ствии жесткого рентгеновского излуче­ния с электронами вещества. Поскольку энергия кванта в этом случае много больше работы выхода, электроны можно считать практически свободными.

Рис. 1.3

П оглощение фотона свободным электроном невозможно. В самом деле, запишем законы сохранения энергии и импульса для такого процесса

( 1. 6)

откуда получаем запрещенную релятивистской теорией скорость электрона, превышающую скорость света .

Поэтому процесс взаимодействия свободного электрона с фотоном имеет характер рассеяния. Это явление наблюдалось Комптоном в 1922 г. Он обнаружил, что длина волны рассеянных рентгеновских лучей вне зависимости от вещества больше, чем у падающих..

Объяснение наблюдаемого эффекта было получено на основе представлений о неупругом столкновении фотона и электрона (рис. 1.3). В процессе столкновения световой квант с энергией передает ее часть электрону. В результате энергия рассеянного кванта оказывается меньше начальной энергии . Аналогичным образом происходит уменьшение импульса фотона от величины до . Используя законы сохранения полного импульса и полной энергии в релятивистской форме можно получить формулу Комптона для изменения длины волны светового кванта в результате столкновения:

, (1.7)

где – угол рассеяния фотона (рис. 1.3), l₀= 2,42·10^-12 м – так называемая комптоновская длина волны. Теоретический результат находится в полном согласии с опытом.

Дата добавления: 2015-08-31