Магнитное поле в веществе. Основные уравнения магнитостатики в веществе. Граничные условия

При изучении магнитного поля в веществе различают два типа токов – макротоки и микротоки.

Макротоками называются токи проводимости и конвекционные токи, связанные с движением заряженных макроскопических тел.

Микротоками (молекулярными токами) называют токи, обусловленные движением электронов в атомах, молекулах и ионах.

Магнитное поле в веществе является суперпозицией двух полей: внешнего магнитного поля, создаваемого макротоками и внутреннего, или собственного, магнитного поля, создаваемого микротоками.

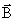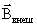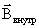Характеризует магнитное поле в веществе вектор , равный геометрической сумме и магнитных полей:

,

(6.3.1)

Количественной характеристикой намагниченного состояния вещества служит векторная величина – намагниченность 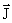, равная отношению магнитного момента малого объема вещества к величине этого объема:

,

(6.3.2)

где 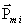– магнитный момент i -го атома из числа n атомов, в объеме Δ V.

Для того чтобы связать вектор намагниченности среды 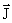с током 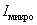, рассмотрим равномерно намагниченный параллельно оси цилиндрический стержень длиной h и поперечным сечением S (рис. 6.3, а). Равномерная намагниченность означает, что плотность атомных циркулирующих токов внутри материала 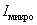повсюду постоянна.

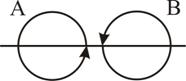
а б в

Рис. 6.3

Каждый атомный ток в плоскости сечения стержня, перпендикулярной его оси, представляет микроскопический кружок, причем все микротоки текут в одном направлении – против часовой стрелки (рис. 6.3, б). В местах соприкосновения отдельных атомов и молекул (А, В) молекулярные токи противоположно направлены и компенсируют друг друга (рис.6.3, в). Нескомпенсированными остаются лишь токи, текущие вблизи поверхности материала, создавая на поверхности материала некоторый микроток 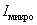, возбуждающий во внешнем пространстве магнитное поле, равное полю, созданному всеми молекулярными токами.

Закон полного тока для магнитного поля в вакууме можно обобщить на случай магнитного поля в веществе:

,

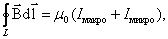(6.3.3)

где 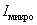и – алгебраическая сумма макро- и микротоков сквозь поверхность, натянутую на замкнутый контур L.

Как видно из рисунка 6.4, вклад в 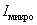дают только те молекулярные токи, которые нанизаны на замкнутый контур L.

Рис. 6.4

Алгебраическая сумма сил микротоков связана с циркуляцией вектора намагниченности соотношением

,

(6.3.4)

тогда закон полного тока можно записать в виде

,

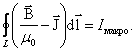(6.3.5)

Вектор

называется напряженностью магнитного поля.

Таким образом, закон полного тока для магнитного поля в веществе утверждает, что циркуляция вектора напряженности магнитного поля вдоль произвольного замкнутого контура L равна алгебраической сумме макротоков сквозь поверхность, натянутую на этот контур:

,

(6.3.6)

Выражение (6.3.6) – это закон полного тока в интегральной форме. В дифференциальной форме его можно записать:

,

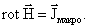(6.3.7)

Намагниченность изотропной среды с напряженностью связаны соотношением:

,

(6.3.8)

где – коэффициент пропорциональности, характеризующий магнитные свойства вещества и называемый магнитной восприимчивостью среды. Он связан с магнитной проницаемостью соотношением .

Уравнения магнитостатики в среде[править | править вики-текст]

Уравнения «для вакуума», приведенные в начале статьи, являются наиболее фундаментальными и простыми (в принципе) уравнениями магнитостатики.

Однако если речь идет о вычислении магнитного поля в среде магнетика, более удобными для практических вычислений, а до некоторой степени и в теоретическом плане, являются менее фундаментальные, однако хорошо приспособленные к этой ситуации, так называемые уравнения для среды (или в среде).

· Говоря о терминологии, следует заметить, что термины уравнения для вакуума и уравнения для среды можно считать в заметной мере условными^[3], однако эта терминология имеет довольно ясное оправдание (см. предыдущее примечание); кроме того, она достаточно устоявшаяся и поэтому не приводит к путанице.

Итак, уравнения для среды используются в магнитостатике для того, чтобы исследовать магнитное поле в случае, когда всё пространство или некоторые его области заполнено магнитной средой (магнетиками). Подразумевается обычно, что среда рассматривается макроскопически (то есть микроскопические поля — поля на атомных масштабах — усредняются, атомные, молекулярные токи и магнитные моменты также рассматриваются только в их совокупности). На микроскопическом уровне действуют^[4] фундаментальные уравнения для вакуума, описанные в статье выше, поэтому в контексте исследования в среде уравнения для ваккма называются также микроскопическими уравнениями в противоположность самим макроскопическим уравнениям для поля в среде.

Формулы для действия поля на движущийся заряд (силы Лоренца) или на ток (силы Ампера) для случая магнитных сред сохраняются полностью неизменными, такими же, как и для вакуума.

Что касается остальных уравнений, они претерпевают для среды определенные изменения по сравнению с вакуумом (имеются в виду, конечно, макроскопические уравнения, микроскопические остаются теми же, что и для вакуума).

В принципе, можно вводить эти изменения по-разному^[5], но весьма общий, традиционный и удобный подход, являющийся общепринятым и стандартным^[6]: записать уравнения с использованием вспомогательной физической величины напряженность магнитного поля , специально вводимой в этом случае.

, где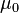

— в системе СИ,

— в системе СГС.

· Здесь — вектор намагниченности, характеризующий магнитную поляризацию среды.

Смысл её введения состоит в том, что с её помощью можно переписать все основные уравнения в виде, очень похожем на тот, что имеют фундаментальные уравнения (для вакуума), а всё касающееся реальной среды поместить по возможности в отдельное уравнение, что позволяет лучше логически структурировать задачу. В сравнительно простых, но важных случаях, к которым относится и практически вся магнитостатика, это удается сделать настолько хорошо, что, в принципе, действительно всё, касающееся конкретной среды, оказывается полностью спрятано в единственную зависимость — зависимость намагниченности от намагничивающего поля (то есть, в принципе, в одну-единственную формулу)^[7] вида (для случая ферромагнетиков, если требовать точности описания, несколько сложнее, но ненамного).

При этом, что также ценно, уравнения для вакуума становятся частным случаем уравнений для среды (случаем среды с всегда нулевой намагниченностью).

· В простейшем, но практически важном случае линейного^[8] отклика среды на намагничивающее поле, просто пропорционально , а если среда изотропна по своим магнитным свойствам, то это сводится просто к умножению на число:

в СИ^[9].

Граничные условия. При переходе через границу раздела двух магнетиков с различными магнитными проницаемостями μ₁ и μ₂ силовые линии магнитного поля испытывают преломление (рис.11.2). Для того, чтобы выяснить, как происходит преломление линий поля необходимо установить для его нормальных и тангенциальных составляющих граничные условия. Вывод граничных условий для магнитного поля в точности аналогичен выводу граничных условий для электрического поля и основывается на применении основных теорем магнитостатики – теоремы Гаусса и теоремы о циркуляции магнитного поля.

Рис.11.2. К выводу граничных условий для магнитного поля.

Для нормальных составляющих индукции 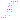теорема Гаусса дает (см. рис.11.2):

,

где S₁ = S₂.

Поток индукции поля через боковую поверхность цилиндра при 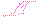(переход к пограничному слою) становится исчезающе малым и им можно пренебречь. Следовательно, при переходе через границу раздела двух однородных магнетиков нормальныесоставляющие индукции магнитного поля непрерывны:

.

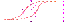Считая, что по границе раздела магнетиков не текут поверхностные токи (I = 0), будем иметь для тангенциальных составляющих напряженности магнитного поля, согласно теореме о циркуляции поля (рис.11.2):

,

где a₁ = а₂ = а.

Составляющие циркуляции поля по коротким сторонам контура обхода границы при (стягивание к границе) исчезают. Таким образом, приходим к выводу, что при переходе через границу раздела двух однородных магнетиков тангенциальные составляющие напряженности магнитного поля непрерывны:

.

Для построения картины преломления силовых линий поля на границе раздела двух магнетиков к полученным граничным условиям необходимо присоединить еще условия, вытекающие из материального уравнения, связывающего векторы 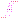и :

и .

Тем самым, задача о преломлении линий поля полностью решается.

Дата добавления: 2015-08-31