Представлення

Юнiкод

Стандарт Юнікоду рекомендує використовувати для представлення римських цифр звичайні латинські букви. Проте стандарт включає також спеціальні символи для римських цифр як частина Числових форм^[en] в області знаків з кодами з U + 2160 по U +2188. Наприклад, MCMLXXXVIII може бути представлено у формі ⅯⅭⅯⅬⅩⅩⅩⅧ. Цей діапазон включає як рядкові, так і прописні цифри для запису чисел від 1 (Ⅰ або I) до 12 (Ⅻ або XII), в тому числі і комбіновані гліфи для складених чисел, таких як 8 (Ⅷ або VIII), головним чином для забезпечення сумісності з східноазіатськими наборами символів в таких промислових стандартах, як JIS X 0213, де ці символи визначені. Комбіновані гліфи використовуються для подання чисел, які раніше складалися з окремих символів (наприклад, Ⅻ замість його представлення як Ⅹ і Ⅱ). На додаток до цього, гліфи існують для архаїчних форм запису чисел 1000, 5000, 10 000, великий зворотної C (Ɔ), пізньої форми запису 6 (ↅ, схожою на грецьку стигму: Ϛ), ранньої форми запису числа 50 (ↆ, схожою на стрілку, що вказує вниз ↓ ⫝⊥ ↓⫝⊥^[1]),), 50 000, і 100 000. Слід зазначити, що маленька зворотна c, ↄ не включена в символи римських цифр, але включена в стандарт Юнікоду як прописна ↄ.

Римські цифрі в Юнікод

Код

A

B

C

D

E

F

Значення^[2]

1 000

U+2160

Ⅰ 2160

Ⅱ 2161

Ⅲ 2162

Ⅳ 2163

Ⅴ 2164

Ⅵ 2165

Ⅶ 2166

Ⅷ 2167

Ⅸ 2168

Ⅹ 2169

Ⅺ 216A

Ⅻ 216B

Ⅼ 216C

Ⅽ 216D

Ⅾ 216E

Ⅿ 216F

U+2170

ⅰ 2170

ⅱ 2171

ⅲ 2172

ⅳ 2173

ⅴ 2174

ⅵ 2175

ⅶ 2176

ⅷ 2177

ⅸ 2178

ⅹ 2179

ⅺ 217A

ⅻ 217B

ⅼ 217C

ⅽ 217D

ⅾ 217E

ⅿ 217F

Значення

1 000

5 000

10 000

50 000

100 000

U+2180

ↀ 2180

ↁ 2181

ↂ 2182

Ↄ 2183

ↅ 2185

ↆ 2186

ↇ 2187

ↈ 2188

Відображення всіх цих символів потребує наявність програмного забезпечення, підтримуючий стандарт Юнікод, и шрифта, який містить відповідні цим символ

8.0 Двійкова система числення

Двійкова система числення — це позиційна система числення, база якої дорівнює двом та використовує для запису чисел тільки два символи: зазвичай 0 (нуль) та 1 (одиницю). Числа, представлені в цій системі часто називають двійковими або бінарними числами.

Завдяки тому, що таку систему доволі просто використовувати в електричних схемах, двійкова система отримала широке розповсюдження у світі обчислювальних пристроїв.

Двійкове число можна представити як послідовність будь-яких об'єктів, які можуть знаходитися в одному з двох можливих станів. Наприклад:

Числа, що можуть приймати значення 0 або 1: 1 0 1 0 0 1 1

Позиції, на яких можуть стояти хрестики або нулики: х о х о о х х

Вузли електричної схеми, які може бути, а може не бути зіструмлено

Ділянки магнітної смужки, які може бути, а може не бути намагнічено

Тощо.

Зазвичай, для позначення двійкових чисел використовують нулі та одиниці. Перші персональні комп'ютери для відображення чисел мали ряд електричних лампочок (кожна з яких, зрозуміло, може або світитися, або бути вимкненою).

8.2Лічба у двійковій системі

Рахувати у двійковій системі не складніше, ніж у будь-якій іншій. Скажімо, у десятковій системі, коли число у поточному розряді сягає десяти, то розряд обнуляється і одиниця додається до старшого. Наприклад: 9+1=10, 44+7=51; Аналогічним чином у двійковій системі: коли число в розряді сягає двох - розряд обнуляється і одиниця додається до старшого розряду. Тобто: 1+1=10. Зверніть увагу, "10" у цьому записі - двійкове число, у десятковій системі це число записується як "2". А десяткове 9+1=10 у двійковій системі буде виглядати так: 1001+1=1010 (після додавання одиниці число в останньому розряді дорівнює двом, тож розряд обнуляється і одиниця додається до передостаннього(старшого) розряду).

8.3Конвертування десяткових чисел у двійкові і навпаки

У системі з основою q число подається у вигляді 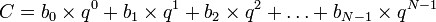(1).

(1)

Підставивши у (1) q=2, одержимо двійкову систему, де число можна записати у вигляді 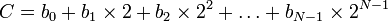(2).

(2)

Де 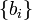- множина цифр числа.

Згідно з виразом (2) запишемо алгоритм розкладу числа С за двійковою системою, який нескладно узагальнити для інших q (мова програмування: Pascal).

Q:=C; { Число }
For i:=0 to N-1 do
begin
b[i]:= Q mod 2; { Остача від ділення на 2 }
Q:= Q div 2; { Цілочисельна частка від ділення на 2 }
end;

Дата добавления: 2015-08-31