Картографические проекции, свойства и их виды по характеру искажений

Виды классификаций картографических проекций

Картографические проекции могут классифицироваться по различным признакам:

• По ориентировке картографической сетки в зависимости от положения точки полюса принятой системы координат
• По виду нормальной картографической сетки, при условии что угловые коэффициенты константы
• По виду общих уравнений картографических проекций
• По характеру искажений (свойствам изображения)
• По способам получения проекций

Классификация проекций По ориентировке картографической сетки в зависимости от положения точки полюса принятой системы координат

Зависит от широты (φ₀) и точки полюса используемой системы координат (Q).

При φ₀=90о полюс принятой системы совпадает с географическим полюсом – получаем прямые проекции, в которых сетка меридианов и параллелей λ = const, φ= const имеет наиболее простой вид. – ее называют нормальной. При φ₀=0 – получаем поперечны е проекции, при 0< φ₀<90 – косые.

Классификация проекций По виду нормальной картографической сетки и общих уравнений картографических проекций

Классификация проекций По виду нормальной картографической сетки была разработана в 30-х годах Каврайским. На ее основе предложена новая аналогичная классификация. Рассматриваем одновременно с классификацией проекций по виду общих уравнений картографических проекций, т.к. они тесно связаны и их совместное рассмотрение позволяет получить более наглядное и полное представление о разработанных проекциях.

1. Проекции с параллелями постоянной кривизны

· Параллели прямые линии. Описывается уравнениями, выраженными только в прямоугольной системе координат. Включает 4 класса проекций

a) Цилиндрические проекции (меридианы - равностоящие параллельные прямые, а параллели – параллельные прямые, ортогональные меридианам). Их общие уравнения х= f (φ) и y=βλ

Где β – параметр проекции

b) обобщенные цилиндрические проекции (меридианы – неравностоящие параллельние прямые, а параллели – параллельные прямые,ортогональные меридианам. Об. Ур-е х= f ₁(φ) и х= f₂ (λ)

c) Псевдоцилиндрические проекции (параллели – параллельные прямые, меридианы – кривые или прямые симметричные относительно среднего прямолинейного меридиана.

Об. Ур-я х= f ₁(φ) и х= f₂ (φ,λ)

d) цилиндрическо-конические проекции, в которых параллели изображаются пучком прямых, а меридианы – концентрическими окружностями.

· Конические окружности. Выражаются в системах плоских полярных и прямоугольных координат.

a) Конически епроекции (параллели – концентрические окружности, а меридианы – пучок прямых, исходящих из центра окружности). Углы между меридиаными на проекции δ пропорциональны углам между ними на поверхности эллипсоида (шара). В точке полюса Р имеется разрыв изображения. Ур-я

b) Обобщенные конические проекции (параллели – конц окружности, меридианы - пучок прямых, исходящих из центра окружности). Углы между меридиаными на проекции δ являются функциями этих углов на эллипсоиде (шаре). В точке полюса Р имеется разрыв.

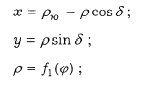
c) Псевдоконические проекции (параллели - концентрические окружности, меридианы – кривые симметричные относительно среднего прямолинейного меридиана). Уравнения

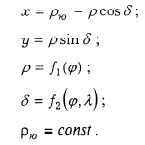
d) Азимутальные проекции (параллели -концентрические окружности, меридианы - пучок прямых, исходящих из центра окружности). В точке полюса отсутствует разрыв изображения. Углы между меридианами на проекции равны углам между ними на шаре (эллипсоиде). Плоские полярные координаты выражаются в функции полярных сфероидических (сферических) координат z=const, a=const. Уравнения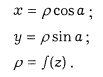

e) Обобщенные азимутальные проекции (параллели -концентрические окружности, меридианы - пучок прямых, исходящих из центра окружности, углы между ними являются функциями этих углов на эллипсоиде, в точке полюса отсутствует разрыв изображения. Меридианы с долготами 0 и 360 совпадают). Уравнения

f) Псевдоазимутальные проекции. Параллели – конц. Окр, в точке полюса нет разрыва изображения. Меридианы с долготами 0 и 360 совпадают и являются либо прямыми либо кривыми, в каждой точке которых они имеют одинаковую кривизну, остальные меридианы – прямые или кривые линии. Уравнения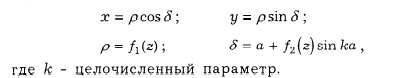

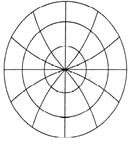
· Эксцентрические окружности. Выражаются в плоских и прямоугольных координатах.

a) Поликонические проекции в широком смысле(параллели – эксцентрические окружности, центры которых находятся на среднем меридиане, а меридианы – кривые симметричные относительно среднего прямолинейного меридиана). Уравнения

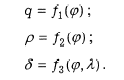
b) Поликонические проекции в узком смысле. Накладывается еще два условия: полярный радиус p=N ctg φ. Частный масштаб длин на среднем меридиане имеет постоянное значение m₀=k, в частности m₀=1.

2) Картографические проекции с параллелями переменной кривизны

· Полиазимутальные проекции и обобщенные полиазимутальные проекции

a) Полиазимутальные проекции. Параллели-эллипсы, меридианы – пучок прямых или кривых, исходящих из центра эллипсов, в точке полюса отсутствует разрыв изображения. Общие уравнения

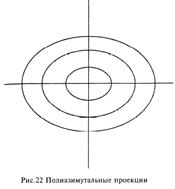
b) Обобщенные полиазимутальные (параллели – кривые произвольной кривизны, а меридианы пучок прямых или кривых, исходящих из точки полюса, в котором нет разрыва изображения). Общие уравнения

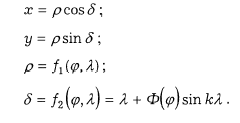
· Обобщенные поликонические, различающиеся изображением параллелей; в виде – эллипсов, парабол, гипербол и параллелями произвольной кривизны, меридианы изображаются кривыми линиями. Обобщенные уравнения

· Полицилиндрические проекции. Параллели и меридианы изображаются кривыми произвольной или заданной кривизны (эллипсами, параболами и гиперболами)

Общие уравнения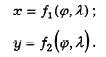

• Проекции произвольных поверхностей, картографическая сетка которых отражает форму картографических поверхностей. Обобщение азимутальных, цилиндрических, конических и др проекций.

• Проекции для создания аноморфированных карт, обладающие дополнительными функциональными возможностями:

a) Варивалентные проекции

b) Переменно-масштабные проекции (при сохранении общего масштаба карты достигается сжатие или растяжение изображения на ее отдельных участках

c) Проекции с измененной метрикой пространства (исп эвклидова метрика и др метрики)

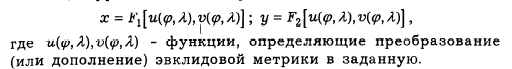
Классификация проекций По характеру искажений (свойствам изображения)

• Равноугольные (картографическая сетка ортогональна, частные масштабы длин не зависят от направлений, но имеются большие искажения площадей)
• Равновеликие (сохраняется постоянным отношение площадей на поверхности эллипсоида или плоскости, но имеются большие искажения углов)
• Произвольные (не выполняется ни равноугольность, ни равновеликость)

Классификация проекций по способам получения

• Решение прямой задачи математической картографии. Определяются отображающие функции, с их использованием получают формулы для вычисления частных масштабов длин, площадей и др характеристик проекции.
• Решение обратной задачи математической картографии осуществляется по заданным значениям характеристик проекции. Определяются прямоугольные координаты искомой проекции и недостающие ее характеристики.

Картографи́ческая прое́кция — математически определенный способ отображения поверхности эллипсоида на плоскости.

Искажение длин — базовое искажение. Остальные искажения из него логически вытекают. Искажение длин означает непостоянство масштаба плоского изображения, что проявляется в изменении масштаба от точки к точке, и даже в одной и той же точке в зависимости от направления.

Это означает, что на карте присутствует 2 вида масштаба:

· Главный, он на карте подписывается, но на самом деле это масштаб исходного эллипсоида, развертыванием которого в плоскость карта и получена.

· Частный масштаб — их бесконечно много на карте, он меняется от точки к точке и даже в пределах одной точки.

Для наглядного изображения частных масштабов вводят Эллипс искажения.

Искажения площадей логически вытекают из искажения длин. За характеристику искажения площадей принимают отклонение площади эллипса искажений от исходной площади на эллипсоиде.

Искажения углов логически вытекают из искажения длин. За характеристику искажений углов на карте принимают разность углов между направлениями на карте и соответствующими направлениями на поверхности эллипсоида.

Искажения формы — графическое изображение вытянутости эллипсоида.

Теория искажений. Искажения в бесконечно малой области около какой-либо точки проекции подчиняются некоторым общим законам. Во всякой точке карты в проекции, не являющейся равноугольной (см. ниже), существуют два таких взаимно перпендикулярных направления, которым на отображаемой поверхности соответствуют также взаимно перпендикулярные направления, это — так называемые главные направления отображения. Масштабы по этим направлениям (главные масштабы) имеют экстремальные значения: μmax= а и μmin= b. Если в какой-либо проекции меридианы и параллели на карте пересекаются под прямым углом, то их направления и есть главные для данной проекции. Искажение длины в данной точке проекции наглядно представляет эллипс искажений, подобный и подобно расположенный изображению бесконечно малой окружности, описанной вокруг соответствующей точки отображаемой поверхности. Полудиаметры этого эллипса численно равны частным масштабам в данной точке в соответствующих направлениях, полуоси эллипса равны экстремальным масштабам, а направления их — главные.

Связь между элементами эллипса искажений, искажениями К. п. и частными производными функций (1) устанавливается основными формулами теории искажений.

Классификация картографических проекций по характеру искажений. В равноугольных (конформных) К. п. масштаб зависит только от положения точки и не зависит от направления. Эллипсы искажений вырождаются в окружности. Примеры — проекция Меркатор, Стереографическая проекция.

В равновеликих (эквивалентных) К. п. сохраняются площади; точнее, площади фигур на картах, составленных в таких проекциях, пропорциональны площадям соответствующих фигур в натуре, причём коэффициент пропорциональности — величина, обратная квадрату главного масштаба карты. Эллипсы искажений всегда имеют одинаковую площадь, различаясь формой и ориентировкой.

Произвольные К. п. не относятся ни к равноугольным, ни к равновеликим. Из них выделяют равнопромежуточные, в которых один из главных масштабов равен единице, и ортодромические, в которых большие круги шара (ортодромы) изображаются прямыми.

При изображении сферы на плоскости свойства равноугольности, равновеликости, равнопромежуточности и ортодромичности несовместимы. Для показа искажений в разных местах изображаемой области применяют: а) эллипсы искажений, построенные в разных местах сетки или эскиза карты; б) изоколы, т. е. линии равного значения искажений; в) изображения в некоторых местах карты некоторых сферических линий, обычно ортодромий (О) и локсодромий (Л.

Дата добавления: 2015-07-13