Элементы бесконечно малой сферической трапеции, их отображение на плоскости

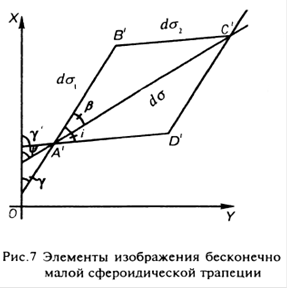
Бесконечно малая сфероидическая трапеция ABCD эллипсоида (рис.5) отображается на плоскость бесконечно малой косоугольной трапецией А'В'С'D' (рис.7), которую с точностью до членов более высоких порядков малости можно принять за бесконечно малый параллелограмм, а ее линейный элемент

dσ=A'С' — за бесконечно малый отрезок прямой.

Элементами этого изображения являются: бесконечно малые отрезки изображения меридиана dcr] - А В и параллели dσ = A'D', которые образуют с осью абсцисс X соответственно углы у и у'; линейный элемент dσ, составляющий с осью X угол ψ; азимут линейного элемента β; углы i в точках проекции между изображениями меридианов и параллелей и площадь изображения бесконечно малой сфероидической трапеции dΣ.

Линейный элемент

Из рис. 7 имеем:

dσ²=dx²+dy² (1)

Полные дифференциалы dx и dy можно представить в виде:

dx=xᵩdϕ+xᵧdλ

dy=yᵩdϕ+yᵧdλ

где xᵩ xᵧ yᵩ yᵧ - обыкновенные или частные производные.

подставив эти дифференциалы в выражение (1)и сгруппировав члены при одинаковых дифференциалах, получим:

dσ²=edϕ²+2fdϕdλ+gdλ (2)

где e, f, g - коэффициенты Гаусса:

e=xᵩ²+yᵩ² f=xᵩxᵧ+yᵩyᵧ g=xᵧ²+yᵩ²

По направлениям мередианов λ=const, dλ=0 и параллелей ϕ=const и dϕ=0, следовательно, с учетом(36):

dσ₁=√edϕ

dσ₂=√gdλ (3)

Углы i между изображениями мередианов и параллелей на проекции

Из рисунка 7 можно записать:

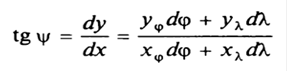(4)

По направлению мередианов dλ=0, угол ψ=ϒ и из (4) получаем:

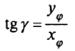(5)

-формулу сближения мередианов.

Соответственно по направлению параллелей dϕ=0, ψ=ϒ' и

(6)

Из рисунка 7 также видно, что i = ϒ'-ϒ, отсюда:

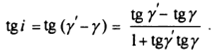
Подставив в это выражение значения (5) и (6), найдем:

(7)

Обозначим числитель 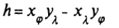(8) и отметим, что он равен функциональному определителю:

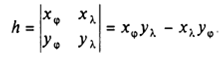
Формула (7) принимает вид: (9)

Определим значения cos i и sin i. Для этого вначале составим функцию eg-f². Используя коэффициенты Гаусса(2), получим

(10)

При этом из двух знаков перед корнем берем знак плюс, так как в математической картографии всегда используются только положительные значения h.

Теперь, если записать

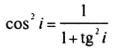
и подставить в это выражение значения (10) (9), то в результате найдем искомые функции:

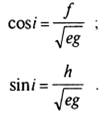(11, 12)

В этих формулах угол i считается северо-восточным в том же направлении, как идет счет азимутов. Его четверть определяется знаком при величине f.

Если f > 0, то i < 90 - угол лежит в первой четверти.

Если f <0, то i > 90 - угол лежит в второй четверти

При f = 0 угол i=90 - меридианы и параллели изображаются ортогональными линиями.

Таким образом выражение

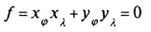(13)

является условием ортогональности картографической сетки на проекции.

Поскольку сетка часто изображается неортогонально, то нередко возникает вопрос о величине отклонения угла i от прямого. Обозначим ε = i -90, тогда из формулы (9)

(14)

Азимут β линейного элемента d σ на проекции

Значение азимута β линейного элемента dσ нетрудно определить, записав из рис.7

β=ψ-ϒ

и

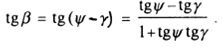
Учитывая формулы,

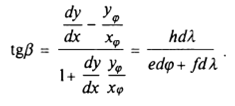
отсюда найдем:

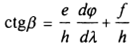
Но из выражения ()

следовательно, предыдущая формула принимает вид:

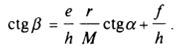(15)

Выражение устанавливает связь азимутов β и α линейных элементов на плоскости и на поверхности эллипсоида.

Дата добавления: 2015-07-13