Основные понятия. Рассмотрим частный случай уравнения Лагранжа при Уравнение (2.25) принимает вид

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ВЫСШИХ ПОРЯДКОВ

Уравнение Клеро

Рассмотрим частный случай уравнения Лагранжа при Уравнение (2.25) принимает вид

и называется урaвнeниeм Клеро. Положив y^'=р, получаем:

Дифференцируя по х, имеем:

Если 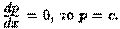Поэтому, с учетом (2.30), ДУ (2.29) имеет общее решение

Если то получаем частное решение уравнения в параметрической форме:

Это решение - особое решение уравнения Клеро: оно не содержится в формуле общего решения уравнения.

Пример 2.13. Решить уравнение Клеро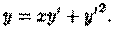

Решение: Общее решение, согласно формуле (2.31), имеет вид y=сх+с². Особое решение уравнения получаем согласно формулам (2.32) в виде

Отсюда следует:

Дифференциальные уравнения порядка выше первого называются ДУ высших порядков. ДУ второго порядка в общем случае записывается в виде

или, если это возможно, в виде, разрешенном относительно старшей производной:

Будем в основном рассматривать уравнение вида (3.2): от него всегда можно перейти к (3.1).

Решением ДУ (3.2) называется всякая функция у=φ(х), которая при подстановке в уравнение обращает его в тождество.

Общим решением ДУ (3.2) называется функция у=φ(х;с₁;с₂), где с₁ и с₂ - не зависящие от х произвольные постоянные, удовлетворяющая условиям:

1. φ(х; с₁; с₂) является решением ДУ для каждого фиксированного значения с₁ и с₂.

2. Каковы бы ни были начальные условия

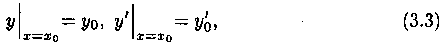
существуют единственные значения постоянных такие, что функция является решением уравнения (3.2) и удовлетворяет начальным условиям (3.3).

Всякое решение уравнения (3.2), получающееся из общего решения у=φ(х;с₁;с₂) при конкретных значениях постоянных называется частным решением.

Решения ДУ (3.2), записанные в виде называются общим и частным интегралом соответственно.

График всякого решения ДУ второго порядка называется интегральной кривой. Общее решение ДУ (3.2) представляет собой множество интегральных кривых; частное решение - одна интегральная кривая этого множества, проходящая через точку (х_о; у_о) и имеющая в ней касательную с заданным угловым коэффициентом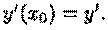

Переписав ДУ (3.1) в виде

видим, что ДУ второго порядка устанавливает связь между координатами точки (х; y) интегральной кривой, угловым коэффициентом k=y^' касательной к ней и кривизной в точке (х; y). В этом состоит геометрическое истолкование ДУ второго порядка.

Как и в случае уравнения первого порядка, задача нахождения решения ДУ (3.2), удовлетворяющего заданным начальным условиям (3.3), называется задачей Коши.

Теорема 3.1 (существования и единственности задачи Коши). Если в уравнении (3.2) функция ƒ(х;y;у^') и ее частные производные ƒ'_y и ƒ'_y' непрерывны в некоторой области D изменения переменных x, y и y', то для всякой точки существует единственное решение у=φ(х) уравнения , удовлетворяющее начальным условиям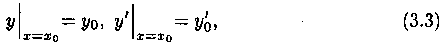

Примем теорему без доказательства.

Аналогичные понятия и определения имеют место для ДУ n-го порядка, которое в общем виде записывается как

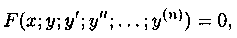или

если его можно разрешить относительно старшей производной. Начальные условия для ДУ (3.4) имеют вид

Общее решение ДУ n-го порядка является функцией вида y=φ(х;с₁;с₂;...;с_n), содержащей n произвольных, не зависящих от х постоянных.

Решение ДУ (3.4), получающееся из общего решения при конкретных значениях постоянных с₁=с₀₁, с₂=с₀₂,..., с_n=c_0n, называется частным решением.

Задача Коши для ДУ n-го порядка: найти решение ДУ (3.4), удовлетворяющее начальным условиям (3.5).

Проинтегрировать (решить) ДУ n-го порядка означает следующее: найти его общее или частное решение (интеграл) в зависимости от того, заданы начальные условия или нет.

Задача нахождения решения ДУ n-го порядка сложнее, чем первого. Поэтому рассмотрим лишь отдельные виды ДУ высших порядков.

Дата добавления: 2017-01-13