Рівняння в повних диференціалах

Рівняння Рікатті – Буля.

Рівняння Бернуллі.

Означення. Рівняння виду y′=a(x) y+ b (х) у , n 1 називається рівнянням Бернуллі.

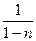Рівняння Бернуллі зводиться, за допомогою заміни невідомої функції, до лінійного рівняння. Представимо рівняння у вигляді =a(x) + b (х). Нехай u= , тоді u′= (1-n) y′ і = u′.

Отже, підставляючи у вихідне рівняння отримаємо 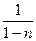u′= a(x)u+ b(х) - лінійне рівняння відносно u.

Означення. Рівняння виду y′+a(x) y+ b (х) у 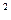=f(x) називається рівнянням Рікатті – Буля.

Загальний розв’язок рівняння не важко знайти якщо відоме яке-небудь рішення рівняння. Дійсно, якщо - який-небудь розвязок рівняння, то розглянемо заміну y= +z, де z – невідома функція. Підставляючи у рівняння отримаємо , або , . Отже відносно z маємо рівняння Бернуллі .

Означення. Рівняння називають рівнянням в повних диференціалах, якщо ліва частина рівняння є повним диференціалом деякої функції.

Необхідною і достатньою умовою (згідно з курсом математичного аналізу) для того щоб вираз 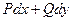був повним диференціалом у деякій області є неперервність функції їх частинних похідних у цій області та виконання рівності .

Нехай рівняння в повних диференціалах, до його можна переписати у вигляді 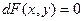(), отже F(x,y)=c – загальне рішення рівняння.

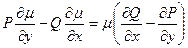Якщо рівність не виконується то може так статись, що існує (інтегруючий множник) для якого рівняння є рівнянням у повних диференціалах. Тоді розв’язок рівняння (що випливає з умови ). Зауважимо, що якщо вираз залежить тільки від однієї змінної х або у, то і можна шукати як таке,що залежить від тієї ж змінної:

(якщо залежить тільки від х),

(якщо залежить тільки від у).

Дата добавления: 2017-01-13