
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Огибаюча сімейства кривих. Рівняння Клеро
|
|
|
|
Приклади.
1) y′=  , (0;0) – особлива точка, оскільки f (х, у) =
, (0;0) – особлива точка, оскільки f (х, у) =  в точці (0,0) терпе розрив. Розв’язуючи рівняння отримаємо
в точці (0,0) терпе розрив. Розв’язуючи рівняння отримаємо  ,
,  і ln|y|=2ln|x|+lnc. Отже загальний розв’язок має вигляд y=cx
і ln|y|=2ln|x|+lnc. Отже загальний розв’язок має вигляд y=cx 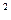 . Таким чином через точку (0,0) проходить нескінченно багато рішень(параболи). Точку такого типу називають вузол.
. Таким чином через точку (0,0) проходить нескінченно багато рішень(параболи). Точку такого типу називають вузол.
2) y′=  ((0;0) – особлива точка). Розв’язуючи рівняння отримаємо
((0;0) – особлива точка). Розв’язуючи рівняння отримаємо  ,
,  і ln|y|=ln
і ln|y|=ln  , отже y=
, отже y=  . Тобто через точку (0,0) не проходить ні один розв’язок (гіпербола). Таку точку називають сідло.
. Тобто через точку (0,0) не проходить ні один розв’язок (гіпербола). Таку точку називають сідло.
3) y′= 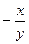 ((0;0) – особлива точка). Розв’язуючи отримаємо загальний розв’язок: уdy=-хdx,
((0;0) – особлива точка). Розв’язуючи отримаємо загальний розв’язок: уdy=-хdx, 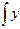 dy=-
dy=-  хdх, отже y
хdх, отже y 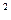 =-x
=-x 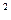 +с або y
+с або y 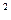 + x
+ x 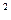 =с. Через точку (0,0) не проходить ні один розв’язок (коло). Таку точку називають центр.
=с. Через точку (0,0) не проходить ні один розв’язок (коло). Таку точку називають центр.
4) y′= 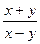 ((0;0) – особлива точка). Загальний розв’язок однорідного рівняння має вигляд x²+y²=с
((0;0) – особлива точка). Загальний розв’язок однорідного рівняння має вигляд x²+y²=с  або у полярних координатах
або у полярних координатах  =с
=с  . Через точку (0,0) теж не проходить ні один розв’язок (спіраль). Таку точку називають фокус.
. Через точку (0,0) теж не проходить ні один розв’язок (спіраль). Таку точку називають фокус.
Самостійно привести зображення кожної з вказаних ситуацій.
Друга умова з порушенням якою зв’язані особливі точки це умова Ліпшица, або обмеженість  , тобто особливі точки можуть з’явитися у точках при наближені до яких
, тобто особливі точки можуть з’явитися у точках при наближені до яких  необмежено росте, або в котрих виконується рівність
необмежено росте, або в котрих виконується рівність  .
.
Означення. Крива називається особою, якщо всі точки кривої є особливими. Якщо особлива крива є рішенням диференціального рівняння, вона називається особливим рішенням.
Приклад. Розглянемо рівняння y′= 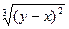 +1. Оскільки
+1. Оскільки  то
то  виконується для точок, що задовольняють рівності у=х – особливе рішення. Той факт, у=х рішення нескладно отримати підставляючи у=х до рівняння.
виконується для точок, що задовольняють рівності у=х – особливе рішення. Той факт, у=х рішення нескладно отримати підставляючи у=х до рівняння.
Знайдемо загальне рішення даного рівняння. Для цього введемо заміну z=y – х, z′=y′ - 1 і y′= z′+1, отже z′+1=  +1. Розв’язуючи останнє рівняння отримаємо
+1. Розв’язуючи останнє рівняння отримаємо 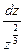 =dx,
=dx,  =∫dx, тобто 3
=∫dx, тобто 3  =x+c, або
=x+c, або  =
=  x +c і на кінець z= (
x +c і на кінець z= ( x +c) ³. Загальний розв’язок рівняння має вигляд y=x+ (
x +c) ³. Загальний розв’язок рівняння має вигляд y=x+ ( x +c) ³. Кожна крива цього сімейства проходить через точку кривої у=х і навпаки через кожну точку (
x +c) ³. Кожна крива цього сімейства проходить через точку кривої у=х і навпаки через кожну точку ( ) кривої у=х проходить деяка крива сімейства, при відповідному
) кривої у=х проходить деяка крива сімейства, при відповідному  (самостійно зробити зображення сімейства та у=х), отже
(самостійно зробити зображення сімейства та у=х), отже 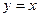 особливий розв’язок рівняння.
особливий розв’язок рівняння.
Означення. Нехай F(x,y,c)=0 сімейство кривих. Тоді L називається огибаючою цього сімейства якщо в кожній своїй точці вона дотикається лінії сімейства і кожна крива сімейства дотикається до L.
Якщо F(x,y,c)=0 є загальним рішенням диференціального рівняння  , то тоді огибаюча сімейства теж є рішенням даного рівняння. Оскільки дотична до огибаючої у довільній точці збігається з дотичною, проведеною до кривої даного сімейства, що дотикається огибаючої у даній точці, то дотична до огибаючої збігається з напрямком, що задається диференціальним рівнянням у даній точці. Отже огибаюча є інтегральною кривою, тобто рішенням. Оскільки через будь-яку точку огибаючої проходить два рішення (огибаюча та деяке рішення з сімейства), то огибаюча – особливе рішення.
, то тоді огибаюча сімейства теж є рішенням даного рівняння. Оскільки дотична до огибаючої у довільній точці збігається з дотичною, проведеною до кривої даного сімейства, що дотикається огибаючої у даній точці, то дотична до огибаючої збігається з напрямком, що задається диференціальним рівнянням у даній точці. Отже огибаюча є інтегральною кривою, тобто рішенням. Оскільки через будь-яку точку огибаючої проходить два рішення (огибаюча та деяке рішення з сімейства), то огибаюча – особливе рішення.
Якщо F(x,y,c)=0 сімейство, то огибаючу його визначають з системи:  .
.
Приклад. Для рівняння  загальне рішення має вигляд y=x+
загальне рішення має вигляд y=x+  .
.
Знайдемо огибаючу до загального рішення з системи:  ,
, 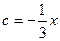 , отже у=х.
, отже у=х.
у=х - огибаюча загального рішення рівняння, отже є особливим рішенням.
Означення. Рівняння виду y=xy′+ 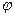 (у′) називається рівнянням Клеро.
(у′) називається рівнянням Клеро.
Знайдемо загальний розв’язок та особливий розв’язок рівняння Клеро. Розглянемо заміну у′=p, тоді y=xp+ 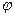 (p) і у′=p+xp′+p′
(p) і у′=p+xp′+p′ 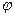 ′(p), враховуючи заміну отримаємо p=p+xp′+p′
′(p), враховуючи заміну отримаємо p=p+xp′+p′ 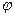 ′(p) або
′(p) або
p′ (x+ 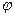 ′ (p)) =0. Остання рівність виконується у двох випадках:
′ (p)) =0. Остання рівність виконується у двох випадках:
1) p′=0, тобто p=c і загальний розв’язок має вид y=cx+ 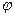 (c);
(c);
2) 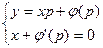 , тобто рішення є огибаюча загального розв’язка
, тобто рішення є огибаюча загального розв’язка  , яку знаходимо з системи
, яку знаходимо з системи  .
.
Приклад. Знайти загальне та особливе рішення рівняння y=xy′+ (у′) 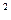 . Загальний розв’язок має вигляд y=cx+ c
. Загальний розв’язок має вигляд y=cx+ c 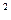 . Огибаючу знаходимо з системи
. Огибаючу знаходимо з системи  . Отже c=
. Отже c=  і y=
і y= 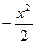 +
+ 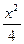 або y=
або y=  . Самостійно розглянути рівняння Лагранжа.
. Самостійно розглянути рівняння Лагранжа.
|
|
|
|
|
Дата добавления: 2017-01-13; Просмотров: 322; Нарушение авторских прав?; Мы поможем в написании вашей работы!