
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Системи диференціальних рівнянь. Теорема існування та єдиності
|
|
|
|
Лекція №5. Системи диференціальних рівнянь першого порядку. Теорема існування та єдиності розв’язку задачі Коші. Рівняння п-го порядку
Задачі для самостійної роботи.
Задачі.
Практичне заняття №4. Рівняння Клеро
Необхідні відомості: 1. Особливі точки та рішення.
2. Означення огибаючої сімейства кривих та спосіб їх знаходження.
3. Рівняння Клеро та Лагранжа.
Знайти загальні й особливі рішення рівнянь Клеро.
1. 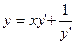
2. 
3. 
4. 
5. Площа трикутника, утвореного дотичній до шуканої лінії й осями координат, є величина постійна. Знайти лінію. 6. Знайти лінію, дотичні до якої відтинають на осях координат відрізки, сума яких дорівнює 2а.
Знайти особливі рішення рівнянь, застосовуючи той же прийом, який використовується у випадку рівнянь Клеро.
1. 
2. 
3. 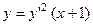
4. 
5. 
6. 
7. 
8. 
9. Знайти лінію, для якої площа прямокутника, що має сторонами дотичну й нормаль у будь-якій точці, дорівнює площі прямокутника зі сторонами, рівними по довжині абсцисі й ординаті цієї точки.
10. Знайти лінію, для якої добуток відстаней будь-якій дотичній до двох даних точок постійний.
Означення. Система рівнянь

де х незалежна змінна, 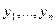 невідомі функції від х, а
невідомі функції від х, а  - похідні
- похідні 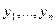 відповідно, називається системоюдиференціальних рівнянь першого порядку.
відповідно, називається системоюдиференціальних рівнянь першого порядку.
Означення. Набір функцій (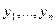 ) будемо називати рішенням системи, якщо при підстановці в систему диференціальних рівнянь отримаємо вірні тотожності.
) будемо називати рішенням системи, якщо при підстановці в систему диференціальних рівнянь отримаємо вірні тотожності.
Розглянемо задачу: знайти рішення  системи
системи
 , що задовольняє умовам
, що задовольняє умовам  ,…,
,…,  така задача називається задачею Коші для системи рівнянь.
така задача називається задачею Коші для системи рівнянь.
Теорема (існування та єдиності). Нехай функції f  (х,
(х, 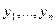 ),…,f
),…,f 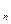 (х,
(х, 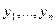 ) визначені і неперервні на області
) визначені і неперервні на області  і по змінним
і по змінним 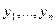 задовольняють умові Ліпшица, тобто |f
задовольняють умові Ліпшица, тобто |f  (х,
(х, 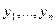 )-f
)-f  (х,
(х,  )|≤N
)|≤N  |
|  |, для будь-яких (
|, для будь-яких (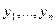 ) і (
) і ( ).Тоді існує h таке, що для х
).Тоді існує h таке, що для х  , задача Коші має єдине рішення, графік якого не виходить з області D; h<max(a,
, задача Коші має єдине рішення, графік якого не виходить з області D; h<max(a,  ), (| f
), (| f  |≤M,
|≤M,  ).
).
Доведення теореми аналогічно доведенню теореми існування та єдиності для одного рівняння. Різниця лише у тому, що замість функції розглядаються набори функцій ( ) і відповідно
) і відповідно  - простір неперервних наборів графіки яких не виходять за межі області D.
- простір неперервних наборів графіки яких не виходять за межі області D.
Зауважимо, що умова Ліпшица буде виконуватися, якщо всі похідні  (i,j=1,…,n) обмежені на області D.
(i,j=1,…,n) обмежені на області D.
|
|
|
|
|
Дата добавления: 2017-01-13; Просмотров: 757; Нарушение авторских прав?; Мы поможем в написании вашей работы!