Математические модели в инженерной практике 1 страница

А.Г.СЕМЕНОВ

Сагалбеков Е.У., Зотова Л.П.

Сдано в набор 25.06.2015 Подписано в печать 25.07.2015

Формат 60 х 84 1/ 16 Заказ № 569

Усл. печ. л. 16,13 Тираж 50 экз

_________________________________________________________________________

Издательство Казахского агротехнического университета им. С. Сейфуллина, 2015 г 010011, г.Астана, пр.Жеңіс 62 а, тел. 39 39 17

Учебное пособие для студентов механических специальностей

заочной формы обучения

КЕМЕРОВО 2003

УДК 519.6: 519.233

Печатается по решению Редакционно-издательского совета Кемеровского технологического института пищевой промышленности

Рецензенты:

- зав. кафедрой автоматизации исследований и технической кибернетики Кемеровского государственного университета, профессор, доктор техн. наук В.Я.Карташов;

- профессор кафедры горных машин и комплексов Кузбасского государственного технического университета, доктор техн. наук Ю.Г.Полкунов.

Семенов А.Г. Математические модели в инженерной практике: Учебное пособие. – Кемеровский технологический институт пищевой промышленности. - Кемерово, 2003. – 96 с.

ISBN 5-89289-299-9

В учебное пособие включены: краткий конспект лекций, описания лабораторных и контрольных работ и задания для их выполнения, программа зачета. Теоретическая часть включает описание методов решения прикладных математических задач. Изложение материала ориентировано на практическую работу студентов. Теоретическая часть снабжена иллюстрациями и примерами.

Илл. – 22. Табл. – 25. Библ. назв. – 6.

ISBN 5-89289-299-9 Ó Кемеровский технологический институт

пищевой промышленности, 2003

I. ОГЛАВЛЕНИЕ

I. ОГЛАВЛЕНИЕ.. 3

II. РАБОЧАЯ ПРОГРАММА КУРСА "МАТЕМАТИЧЕСКИЕ МОДЕЛИ В ИНЖЕНЕРНОЙ ПРАКТИКЕ". 5

III.ЛЕКЦИОННЫЙ КУРС.. 6

3.1. Основные понятия математического моделирования. 6

3.2. Решение нелинейных алгебраических уравнений. 10

3.3. Решение систем линейных алгебраических уравнений. 13

3.4. Исследование сеточных функций. 16

3.5. Численное решение обыкновенных дифференциальных уравнений 22

3.6. Моделирование процессов, приводящих к дифференциальным уравнениям в частных производных. 28

3.7. Дифференциальное уравнение теплопроводности. 29

3.8. Краевые задачи для уравнений в частных производных. 33

3.9. Оптимизационные модели. Основные понятия и определения. 37

3.10. Схема решения задач оптимизации. 39

3.11. Численные методы решения задач. 40

безусловной одномерной оптимизации. 40

3.12. Многомерная безусловная оптимизация. 43

3.13. Условная оптимизация при решении инженерных задач. 44

3.14. Линейное программирование. 44

3.15. Обработка экспериментальных данных. 49

IV. ЛАБОРАТОРНЫЕ РАБОТЫ... 53

4.1. Работа 1:Табулирование функций. 53

4.2.Работа 2: Решение трансцендентных алгебраических уравнений. 61

4.3. Работа 3. Решение систем линейных алгебраических уравнений. 65

4.4. Работа 4: Решение задач линейного программирования. 69

4.5. Работа 5. Обработка экспериментальных данных. 77

V. КОНТРОЛЬНЫЕ РАБОТЫ... 83

5.1. Контрольная работа № 1. 84

5.2. Контрольная работа № 2. 89

VI. ВОПРОСЫ К ЗАЧЕТУ.. 95

VII.БИБЛИОГРАФИЧЕСКИЙ СПИСОК. 96

II. РАБОЧАЯ ПРОГРАММА КУРСА "МАТЕМАТИЧЕСКИЕ МОДЕЛИ В ИНЖЕНЕРНОЙ ПРАКТИКЕ"

№	Содержание темы	Объем	Литература
	Основные понятия моделирования. Классификация математических моделей. Этапы процесса создания математической модели	Определяется учебным планом
	Основные типы математических задач, возникающие в процессах моделирования природных и технических систем.	- " -
	Решение алгебраических уравнений и систем линейных уравнений.	- " -	[3], с. 60-65, 72-75, 92-99
	Исследование сеточных функций. Численное дифференцирование и интегрирование.	- " -	[3], c. 29-33, 48-54
	Решение обыкновенных дифференциальных уравнений. Понятие об основных типах задач для обыкновенных дифференциальных уравнений.	- " -	[3], c. 100-106
	Дифференциальные уравнения в частных производных.	- " -	[5], c. 526-533
	Оптимизационные задачи. Условная и безусловная, одномерная и многомерная оптимизация.	- " -	[3], c. 110-114, 122-128
	Задачи линейного программирования	- " -
	Основы обработки экспериментальных данных. Метод наименьших квадратов.	- " -	[3], c. 42-46

III.ЛЕКЦИОННЫЙ КУРС

3.1. Основные понятия математического моделирования

Моделью какой-либо системы называется другая система, изучение которой позволяет сделать выводы о поведении исходной системы (оригинала). Смысл построения моделей состоит в том, что исследование модели является более простым, нежели исследование оригинала (достаточно часто прямое исследование оригинала может оказаться и вовсе невозможным по различным причинам).

Виды моделей:

1. Словесные (описания)

2. Натурные (макеты)

3. Аналоговые. Аналоговое моделирование основано на том, что различные физические явления могут описываться одинаковыми математическими соотношениями. Так, дифференциальное уравнение Лапласа

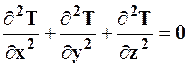
описывает:

· распределение электрического потенциала в области пространства;

· стационарное распределение температуры в сплошной среде;

· течение идеальной (лишенной внутреннего трения) жидкости.

Поэтому можно заменить, например, исследование распределения температуры в теле сложной формы измерением распределения электрического потенциала в некоторой области, выполнить которое существенно проще.

4. Математические модели (ММ) основаны на анализе и решении математических соотношений (уравнений, систем уравнений, неравенств), описывающих характеристики системы-оригинала.

Этапы создания ММ:

1. Постановка задачи. На этом этапе необходимо определить цель моделирования, выявить свойства оригинала, исследование которых важно, и те свойства, знание которых несущественно в рамках проводимого исследования и которыми, следовательно, можно пренебречь;

2. Составление математического описания объекта. По способу получения математических соотношений, описывающих ММ, модели делятся на:

1) теоретические или феноменологические, в которых необходимые математические соотношения получаются на основе анализа физических законов, описывающих процессы в системе, материальных балансов и других объективно существующих связей и закономерностей;

2) эмпирические, в которых связи характеристик системы определяются экспериментально;

3) полуэмпирические, или смешанные; в таких моделях основные математические соотношения получаются на основе объективных закономерностей, но при их построении приходится делать ряд допущений и вводить в соотношения неопределенные коэффициенты, значения которых определяются экспериментально.

Чисто эмпирические модели имеют ряд недостатков. Во-первых, для их построения приходится строить макет устройства и проводить достаточно большое количество экспериментов. Во-вторых, само устройство является в этом случае "черным ящиком" – мы можем измерить только связь между значениями входных параметров (называемых факторами) и выходных параметров (откликов), но не можем ничего сказать об особенностях происходящих в системе процессов, о том, каким образом ее структура влияет на функционирование и обуславливает именно такую связь "входа" и "выхода". Наконец, эмпирические модели невозможно экстраполировать, то есть, применить за пределами диапазона параметров, уже исследованного экспериментально. Однако, при изучении сложных технических устройств эмпирический подход часто является единственно возможным из-за большого количества взаимовлияющих факторов, объективный учет которых не представляется возможным. Эмпирические модели уже существующих устройств необходимы при создании систем автоматического управления их работой.

3. Решение полученной математической задачи. Оно может быть:

· аналитическим, то есть, представленным в виде алгебраических формул;

· численным, то есть, представленным в виде числовых таблиц и графиков, не описываемых явными алгебраическими формулами.

Получить аналитическое решение задачи удается нечасто и в основном для простейших моделей. Гораздо чаще получают численное решение, причем большинство существующих методов получения численных решений позволяют сделать это со сколь угодно малой погрешностью. Поэтому при дальнейшем использовании модели в процессе проектирования и расчета каких-то технических устройств аналитическое решение не дает преимуществ перед численным, так как численный расчет по любой аналитической формуле все равно ведется с какой-то погрешностью.

4. Проверка адекватности и точности построенной модели. Эти понятия часто смешивают.

Адекватностью называют свойство модели отражать основные качественные особенности поведения оригинала.

Точность – это степень количественной близости значений характеристик модели и оригинала.

Рассмотрим график, показывающий зависимость отклика Y от фактора X для некоей системы и двух моделей этой системы

Про обе модели можно сказать, что они адекватно отображают свойства системы-оригинала, однако точность модели 2 заметно выше, чем точность модели 1.

Проверку адекватности и точности модели осуществляют разными способами. Чаще всего результаты, полученные при помощи модели, сравнивают с данными наблюдения реальной системы или выборочно проведенных экспериментов.

5. Использование модели. Если модель не предназначена для последующего практического применения, то ее создание вообще не имеет смысла. Практически модели природных систем используются для уточнения законов природы, для прогнозирования дальнейшего поведения систем, изучения последствий деятельности человека (модели климата, экологических систем и т.п.). Моделирование технических систем необходимо при их проектировании, поиске путей совершенствования, изучении аварийных ситуаций, автоматизации управления их работой и т.п.

Всевозможные ММ природных и технических систем можно разделить на классы:

1. По отношению к изменению характеристик во времени:

· статические, стационарные – не учитывающие изменение характеристик во времени;

· динамические, нестационарные – учитывающие изменение характеристик во времени;

2. По отношению к распределению параметров в пространстве:

· дискретные – параметры которых "привязаны" к отдельным точкам пространства или отдельным узлам и агрегатам системы (в этом случае анализируются связи между узлами, а их внутреннее устройство не рассматривается);

· континуальные, непрерывные – характеристики которых меняются в пространстве от точки к точке и образуют поля (непрерывные распределения, описываемые функциями координат, а в нестационарных системах еще и времени).

Особый класс ММ – модели экономических систем и процессов.

Разные классы ММ приводят к различным математическим задачам. Так, континуальные модели всегда описываются дифференциальными уравнениями в частных производных. Дискретные модели сводятся к системам алгебраических уравнений в стационарном случае и к обыкновенным дифференциальным уравнениям в нестационарном. При построении ММ и решении соответствующих математических соотношений могут возникать также различные дополнительные проблемы.

Далее рассматриваются способы решения некоторых математических задач, возникающих в ходе математического моделирования технических, технологических и природных систем и процессов.

3.2. Решение нелинейных алгебраических уравнений

Рассмотрим закон Планка, определяющий зависимость интенсивности электромагнитного излучения абсолютно черного тела при температуре излучающего тела Т от длины волны l

. (1)

Определим – при какой длине волны интенсивность излучения максимальна. Для этого приравняем к нулю производную

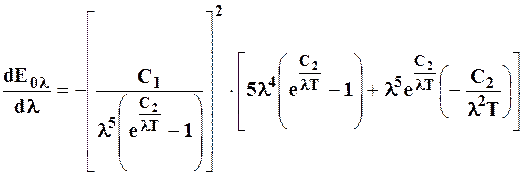
После упрощения задача сводится к решению уравнения

(2)

где обозначено

(3)

Выразить решение этого уравнения в виде замкнутой алгебраической формулы или, как говорят, "в квадратурах", невозможно. Однако найти численное значение его решения не так уж трудно.

Данный пример показывает, каким образом в процессе математического моделирования приходится сталкиваться с решением нелинейных и трансцендентных (содержащих экспоненциальные, логарифмические, тригонометрические и т.п. функции) уравнений. Такие уравнения встречаются в расчетах различных задач теплообмена и других технических и технологических процессов и систем.

Рассмотрим два способа решения нелинейных и трансцендентных уравнений.

1. Метод половинного деления.

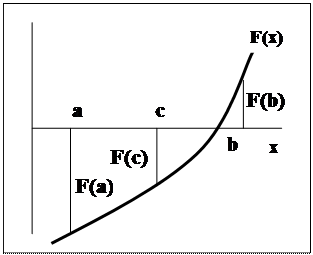
Для начала надо определить ту область числовой оси (отрезок), внутри которой находится корень уравнения. Для этого уравнение приводится к виду:

(4)

Затем функция F(x) табулируется (составляется таблица значений при разных значениях х) и отыскиваются два ближайших друг к другу значения х, при которых значения функции имеют разные знаки. Обозначим эти значения а и b. Затем находим значение функции в точке x = c, являющейся серединой отрезка [a,b]. Корень уравнения может находиться либо в левой половине отрезка, либо в правой. Выбрать нужную половину можно по тому же принципу – на ее концах значения функции должны иметь разные знаки. Потом эту половину снова делим пополам, находим значение функции f(x) в ее середине и выбираем ту из частей, в которой находится корень. Процесс повторяется несколько раз. На каждом шаге первоначальный отрезок [a,b] делится пополам, так что после N повторений процесса длина оставшегося отрезка будет равна D=(b-a)/2^N. За корень уравнения можно принять середину остающегося отрезка, в этом случае погрешность определения корня равна d = ± D/2. Видно, что повторяя процесс несколько раз, можно постепенно уменьшить погрешность определения корня до сколь угодно малой величины.

Такой метод нахождения корня привлекателен своей простотой и безотказностью, так как позволяет найти решение уравнения в любом случае, когда этот корень вообще существует. Недостатком же является относительно медленная сходимость (скорость уменьшения погрешности).

2. Метод последовательных приближений (итераций). Для его использования уравнение надо привести к виду:

. (5)

Например, для уравнения (2) такое преобразование даст:

. (6)

Выберем начальное значение для х, находящееся где-то поблизости от корня уравнения (область, в которой находится корень, определяется так же, как для метода половинного деления). В нашем случае можно принять x₁=5. Подставим это значение в правую часть уравнения (6):

.

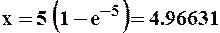Это будет следующее приближение для корня: x₂. Вновь подставим его в правую часть уравнения и получим третье приближение:

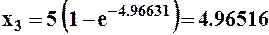
Следующая подстановка дает четвертое приближение корня х₄=4.96512. Пятое приближение получится равным х₅=4.96511. Оно уже не отличается от предыдущего с точностью до четырех знаков после запятой. Если необходимо найти еще более точное значение корня, процесс последовательных приближений можно повторить еще несколько раз.

Видно, что метод последовательных приближений имеет высокую скорость сходимости, поэтому он часто применяется для решения нелинейных и трансцендентных уравнений вручную с помощью калькулятора. Его недостатком является то, что итерационный процесс сходится не всегда, а только в том случае, если на отрезке первоначальной локализации корня [a,b] выполняется соотношение:

. (7)

Проверка выполнения условия (7) бывает затруднена, если функция f(x) имеет сложную структуру. В этом случае итерационный процесс проводят, не проверяя условие, а о наличии или отсутствии сходимости судят по уменьшению или увеличению разницы между двумя последовательно найденными значениями x.

3.3. Решение систем линейных алгебраических уравнений

Модели дискретных статических систем часто описываются системами линейных алгебраических уравнений (СЛАУ) вида:

(8)

Такие системы возникают при расчетах ферменных строительных конструкций (реакции опор и усилия в узлах фермы), распределений электрических токов в сложных электрических цепях, тепловых балансов смежных помещений в отапливаемых или охлаждаемых зданиях и во многих других случаях. Для решения используются следующие основные методы:

1. Метод Гаусса или метод последовательного исключения неизвестных.

Выразим из первого уравнения системы (8) неизвестную величину х₁:

. (9)

Затем подставим это выражение в остальные уравнения системы. Тогда во втором уравнении, например, получится:

(10)

Это уравнение уже не содержит неизвестной величины х₁. Преобразовав подобным образом остальные уравнения системы, получаем систему из (n-1) уравнения с (n-1) неизвестным. Затем из этой системы аналогичным образом исключается неизвестная величина х₂, потом х₃ и т.д. На последнем шаге исключается неизвестная величина х_n-1 и остается уравнение для определения х_n. Обратным ходом по значению х_n находят х_n-1, затем х_n-2 и т.д., вплоть до х₁, определяемого с помощью (9).

Метод Гаусса всегда позволяет найти решение СЛАУ, если оно существует, но он является очень трудоемким. Поэтому его используют, если имеется готовая компьютерная программа его реализации. Также этот метод используется для нахождения решения в различных прикладных пакетах математических расчетов.

2. Методы последовательных приближений.

Предварительно систему необходимо привести к виду:

. (11)

Наиболее просто это можно сделать, выразив из каждого уравнения соответствующее значение x, т.е., принимая:

(12)

Затем выбираются начальные значения х_i, подставляются в правые части уравнений (2) и вычисляются следующие значения, опять подставляются в правые части и т.д., до тех пор, пока два последовательно вычисленных значения любого из неизвестных не окажутся совпадающими друг с другом с заданной точностью. Процесс, таким образом, в принципе не отличается от итерационного процесса решения трансцендентных алгебраических уравнений

В качестве начальных значений x_i обычно принимаются значения свободных членов уравнений d_i.

Существует две разновидности метода последовательных приближений. В методе простых итераций вычисляются сразу все n значений неизвестных и все разом подставляются в правые части уравнений (11). В методе Зейделя каждое вычисленное новое значение очередного неизвестного сразу же начинают подставлять в правые части уравнений вместо старого, что увеличивает скорость сходимости процесса.

Недостатком методов последовательных приближений является то, что итерационный процесс, как правило, сходится только при выполнении определенных условий. В случае системы линейных алгебраических уравнений условие сходимости таково:

(i = 1 … n) (13)

или для исходной системы (8):

(i=1 … n) (14)

Проверка выполнения условий сходимости (14) проводится перед преобразованием системы (8). В случае нарушения условий уравнения меняются местами или уравнение, для которого условие сходимости нарушается, заменяется на линейную комбинацию его с другими уравнениями системы, для которой условие сходимости выполняется. Например, в системе:

(15)

условие сходимости нарушено для второго уравнения. Умножим второе уравнение на 2 и вычтем из полученного уравнения первое уравнение. Получим:

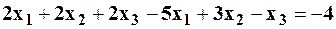, (16)

или

. (17)

Для такого уравнения условие сходимости выполняется:

(18)

Методы последовательных приближений позволяют найти решение СЛАУ довольно быстро, поэтому их часто применяют для расчетов вручную. Достаточно легко также запрограммировать процесс решения для компьютерного расчета.

3.4. Исследование сеточных функций

При математическом моделировании часто приходится иметь дело с так называемыми сеточными функциями. Сеточной будем называть любую функцию y(x), для которой неизвестно ее алгебраическое выражение и которая задана набором своих значений при отдельных значениях аргумента x_i, называемых узлами сетки (i = 0, 1, 2, …, N). Значения сеточной функции в соответствующих узлах будем обозначать y_i. Расстояние между двумя соседними узлами сетки h_i = x_i+1-x_i называется шагом сетки. Мы будем рассматривать сетки с постоянным шагом, когда расстояние между любой парой соседних узлов всегда одинаково.

С сеточными функциями приходится сталкиваться в процессе работы с таблицами тех или иных зависимостей (например, таблицы физических свойств веществ). Численные решения динамических и континуальных ММ также представляются в виде сеточных функций.

Рассмотрим некоторые задачи обработки и исследования сеточных функций.

1. Интерполирование сеточной функции.

Интерполированием называется определение значения сеточной функции при значении аргумента х, лежащем между двумя узлами. Чаще всего такая задача встает при работе с таблицами физических свойств – либо для получения конкретных значений свойств в определенном состоянии, либо для получения алгебраического выражения функциональной зависимости, предназначенного для дальнейшего использования в какой-то более сложной ММ.

Рассмотрим два способа интерполяции.

а) Линейная интерполяция.

Она применяется в основном при расчетах вручную, если необходимо определить по таблицам значения какой-то функции для значения аргумента, которое отсутствует в таблице. Так, если по таблице надо найти значение функции y при значении аргумента x, надо из таблицы выбрать два значения аргумента x₁ и x₂, ближайшие к x, так, что x₁ < x < x₂ и соответствующие им значения функции y₁ и y₂. На отрезке [x₁, x₂] функция y(x) приближенно заменяется на линейную. Тогда вместо искомого значения функции определяется значение линейной функции по формуле, вытекающей из подобия треугольников:

,

т.е.

. (19)

б) Алгебраическая интерполяция. Чаще всего в качестве интерполирующей функции используется полином, степень которого на единицу меньше числа узлов. Определение коэффициентов интерполирующего полинома может быть проведено разными способами (интерполирующий полином в форме Лежандра, Стирлинга, Ньютона и др.), хотя все они дают в конечном итоге один и тот же результат. Рассмотрим непосредственное алгебраическое определение коэффициентов интерполирующего полинома.

Постановка задачи: даны N значений сеточной функции y_i в точках x₀, x₁, x₂, … x_N. Требуется построить полином:

, (20)

принимающий в каждой из точек x_i соответствующее значение y_i.

Решение: пользуясь свойством полинома P(x_i), запишем N+1 равенств:

(21)

Они образуют систему из N+1 линейных алгебраических уравнений для определения N+1 неизвестных коэффициентов полинома a_i. Решив систему одним из способов, разобранных выше, можно построить искомый интерполирующий полином.

Если сеточная функция является достаточно гладкой, о чем можно судить по ее графику, для интерполяции можно использовать не все узлы. В этом случае интерполяционный полином будет давать приближенные значения функции, но погрешность будет сравнительно невелика. Использование полиномов высоких степеней, наоборот, может привести к нежелательным колебаниям значений слагаемых высокой степени и увеличению погрешности интерполяции между узлами сетки.

Дата добавления: 2017-01-13