
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Математические модели в инженерной практике 2 страница
|
|
|
|
2. Дифференцирование сеточной функции. Вспомним определение производной функции y(x):
 . (22)
. (22)
"Переведем" это определение на язык сеточных функций. Если в качестве х рассмотреть один из узлов xi, то значение Dх – это шаг сетки h, а хi+ Dх = xi+1 . При меньшем значении Dх сеточная функция просто не определена. Тогда за производную сеточной функции следует принять выражение:
 (23)
(23)
 |
Это можно проиллюстрировать графически:
Производная графически выражается тангенсом угла наклона касательной к графику функции в узле xi, то есть, прямой I (сплошной). Выражение (23) – это тангенс угла наклона секущей прямой II (пунктирной, проходящей через точки В и С). Видно, что наклон линий I и II отличается друг от друга, так что выражение (23) дает весьма приближенное значение производной.
Значение приращения Dx в выражении (22) может быть и отрицательным, для дифференцируемой функции получится то же значение производной. Тогда для сеточной функции получим выражение:
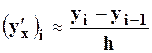 . (24)
. (24)
На рисунке ему соответствует тангенс угла наклона секущей прямой АВ (линии III). Наклон этой прямой тоже заметно отличается от наклона касательной I.
Более точное значение производной получится, если взять среднее арифметическое из значений, даваемых формулами (23) и (24):
 . (25)
. (25)
Это выражение тангенса угла наклона секущей прямой АС (линии IV). Наклон этой прямой гораздо ближе к наклону касательной, чем линий II и III, так что выражение (25) позволяет определить производную существенно точнее.
Используя разложение функции y(x) в ряд Тейлора, можно доказать, что погрешность определения производной выражениями (23) и (24) имеет порядок величины шага h, а у выражения (25) погрешность порядка h2. При малой величине шага сетки погрешность выражения (25) намного меньше, чем у выражений (23),(24). Говорят, что выражение (25) имеет второй порядок точности, тогда как (23) и (24) – выражения первого порядка точности.
3. Интегрирование сеточной функции. Рассмотрим два способа вычисления значения определенного интеграла

- вычисление по формуле трапеций и по формуле Симпсона-Ньютона. Необходимость вычисления определенных интегралов возникает не только в случаях, когда функция y(x) является сеточной, но чаще, если выражение этой функции известно, но является слишком сложным, чтобы интеграл (26) можно было выразить явной формулой (вычислить "в квадратурах"). В обоих случаях для вычисления необходима сетка. Для приближенного вычисления отрезок [a,b] разбивается на малые шаги h равной величины. Количество шагов для рассматриваемых методов: для метода трапеций безразлично, для метода Симпсона-Ньютона оно должно быть четным числом. Узлы сетки:

где N - число шагов. Для каждого узла вычисляется значение функции 
а) Метод трапеций. Вывод расчетной формулы для метода трапеций легко проводится графически, если учесть, что графическим выражением определенного интеграла является площадь под графиком функции y(x):
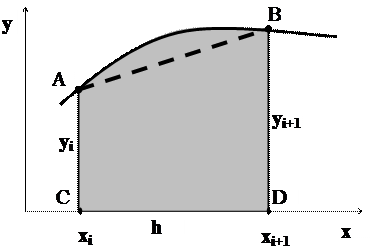 |
На рисунке эта площадь заштрихована. Заменим приближенно функцию y(x) на отрезке [xi, xi+1] отрезкомпрямой АВ и будем искать приближенное значение интеграла на этом отрезке, как площадь трапеции ABDС. Основаниями трапеции служат отрезки АС и BD, длины которых выражают значения функции в узлах: yi и yi+1, а высотой – длина отрезка CD, то есть шаг сетки h. Тогда площадь трапеции (произведение полусуммы оснований на высоту) равна
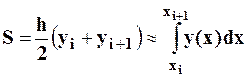 .
.
Если записать эту формулу для каждого шага сетки от x0 = a до xN = b, а затем сложить получившиеся выражения, мы получим расчетную формулу трапеций:
 (26)
(26)
Эта формула широко применяется для приближенного вычисления определенных интегралов как вручную, так и при расчетах на компьютерах.
б) Метод Симпсона-Ньютона. Если вывод формулы трапеций основан на применении линейной интерполяции функции y(x), то формула Симпсона-Ньютона получается, если заменить функцию на двух смежных шагах интерполяционным полиномом второй степени, построенным по трем точкам – узлам xi, xi+1, xi+2 и затем взять интеграл от этого полинома. Приведем эту формулу без вывода:
· для двух шагов:

· для отрезка [a, b]:
 (27)
(27)
Формула Симпсона-Ньютона используется преимущественно в расчетах на компьютерах, так как вычисления по ней программируются так же легко, как и расчет по формуле трапеций, а погрешность вычисления существенно меньше (формула трапеций имеет третий порядок точности, а формула Симпсона-Ньютона – пятый).
3.5. Численное решение обыкновенных дифференциальных уравнений
Обыкновенные дифференциальные уравнения (ОДУ) и системы таких уравнений широко встречаются в математическом моделировании. ОДУ связывает между собой значения независимой переменной (аргумента), искомой величины – функции этого аргумента и производных этой функции. Наибольший порядок производной определяет и порядок уравнения.
ОДУ первого порядка широко встречаются в ММ динамических дискретных систем, ОДУ второго и высших порядков могут возникать и в моделях континуальных стационарных систем, если характеристики системы непрерывно меняются вдоль одной пространственной координаты.
При интегрировании ОДУ появляется ряд неопределенных констант интегрирования, число которых совпадает с порядком уравнения. Для определения этих констант служат начальные и граничные условия.
Начальные условия – это задание определенных связей для искомой функции при начальном значении аргумента (в начальный момент времени, в начальной точке какой-то линейно протяженной пространственной области). Задача отыскания решения системы ОДУ первого порядка с заданными начальными условиями называется в математике задачей Коши.
Граничные условия задаются при двух значениях аргумента. Обычно это условия на границах пространственной области.
Примеры:
а) тело падает с некоторой высоты. Необходимо определить зависимость скорости и положения тела над землей от времени.
 На тело действуют две силы: сила тяжести, равная mg, где m – масса тела, g – ускорение свободного падения, и сила сопротивления воздуха, имеющая две составляющих – силу трения, пропорциональную скорости тела, а также вихревое сопротивление, пропорциональное квадрату скорости. Не вдаваясь в физические подробности, запишем общее сопротивление так: Fсопр=-(av+bv2). Теперь уравнение второго закона Ньютона применительно к телу в проекции на ось Oy запишется (для удобства направим ось Оу вниз):
На тело действуют две силы: сила тяжести, равная mg, где m – масса тела, g – ускорение свободного падения, и сила сопротивления воздуха, имеющая две составляющих – силу трения, пропорциональную скорости тела, а также вихревое сопротивление, пропорциональное квадрату скорости. Не вдаваясь в физические подробности, запишем общее сопротивление так: Fсопр=-(av+bv2). Теперь уравнение второго закона Ньютона применительно к телу в проекции на ось Oy запишется (для удобства направим ось Оу вниз):
 . (28)
. (28)
Скорость тела:
 . (29)
. (29)
Таким образом, движение тела описывается уравнением (штрих, как обычно в математике, обозначает производную):
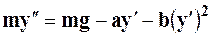 . (30)
. (30)
Оно имеет второй порядок и требует постановки двух начальных условий. Если отсчитывать координату у от начального положения тела и считать, что его движение начинается из состояния покоя, условия примут вид:
 . (31)
. (31)
Задачу можно описать также системой двух уравнений (28), (29), каждое из которых имеет первый порядок. Таким образом, уравнение высокого порядка можно преобразовать в систему уравнений пониженного порядка, принимая производные за новые переменные аналогично (29). Начальные условия в этом случае будут выглядеть:
 . (32)
. (32)
Рассмотренная задача дает пример математической модели физического процесса, описываемого задачей Коши.
 б) для улучшения охлаждения к корпусу теплового двигателя температурой Т0 приварены ребра – тонкие металлические пластины. Необходимо определить распределение температуры вдоль ребра и количество тепла, отводимое с его помощью в окружающую среду.
б) для улучшения охлаждения к корпусу теплового двигателя температурой Т0 приварены ребра – тонкие металлические пластины. Необходимо определить распределение температуры вдоль ребра и количество тепла, отводимое с его помощью в окружающую среду.
Распространение тепла в толще ребра описывается так называемым законом Фурье:
 , (33)
, (33)
где Q – количество тепла, переносимое за 1 сек через сечение ребра площадью F=bH; l -так называемый коэффициент теплопроводности, Т – температура. Количество тепла, отводимое в окружающую среду с участка поверхности ребра длиной dx, равно (Тос – температура окружающей среды):
 .
.
Первое слагаемое в квадратных скобках выражает охлаждение поверхности ребра омывающим его воздухом, второе – отвод тепла путем теплового излучения. Исходя из теплового баланса слоя ребра, ограниченного сечениями, соответствующими значениям координат x и x+dx, можем записать:
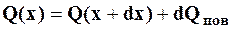 ,
,
откуда

В левой части равенства стоит выражение производной


(так как наличие дифференциала dx указывает на предельный переход при х®0, ср. (22)). С учетом (33) получаем уравнение:
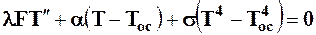 . (34)
. (34)
Это уравнение второго порядка и для него надо поставить два условия. Одно из них очевидно: T=T0 при х=0. Второе условие в теории теплообмена ставится по-разному. Простейший вариант (пригодный для длинных ребер) – считать, что температура конца ребра совпадает с температурой окружающей среды: Т=Тос при х=L. Таким образом, в данной задаче для дифференциального уравнения (34) поставлены граничные условия.
Рассмотрим некоторые методы решения ОДУ. Начнем с методов решения задачи Коши, то есть, численного решения дифференциальных уравнений вида
 (35)
(35)
и систем уравнений вида
 (36)
(36)
с начальными условиями
 или
или 
 (37)
(37)
а) метод Эйлера.
Используя формулу производной сеточной функции (23), можно записать:

Это и есть расчетная формула метода Эйлера. Для решения отрезок оси Ох, на котором надо найти решение уравнения, разбивают на малые шаги h ( создают сетку ), затем в правую часть подставляют значения  и
и  . Это позволяет приближенно определить значение искомой функции y(x) в точке
. Это позволяет приближенно определить значение искомой функции y(x) в точке  . Затем найденные значения
. Затем найденные значения 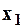 и
и  опять подставляют в правую часть формулы (6), вычисляют
опять подставляют в правую часть формулы (6), вычисляют  и т.д. Если обозначить
и т.д. Если обозначить 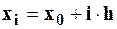 , то формулу (6) можно записать в окончательном виде
, то формулу (6) можно записать в окончательном виде

 (38)
(38)
б) метод Рунге-Кутта. Этот метод основан на использовании представлений производных, имеющих более высокий порядок точности. Вычисление решения в очередном узле проводится по следующим формулам (приводятся без вывода):
 (39)
(39)
где
 (40)
(40)
Оба метода достаточно легко обобщаются на случай систем ОДУ – в этом случае функции в правых частях формул оказываются функциями нескольких переменных, но их значения все равно вычисляются для уже рассчитанных узлов сетки.
Метод Эйлера реализуется существенно легче, чем метод Рунге-Кутта, поэтому его можно применить даже при расчете вручную, однако его точность крайне низка – он имеет первый порядок точности, тогда как метод Рунге-Кутта – четвертый. Поэтому в компьютерных расчетах используется метод Рунге-Кутта или другие методы высокого порядка точности.
Для решения краевых задач применяются разные методы. Рассмотрим самый простой из них – метод пристрелки или стрельбы. Он основан на преобразовании краевой задачи в задачу Коши.
Рассмотрим для примера задачу (34), которую запишем в виде:
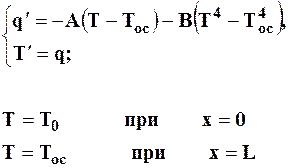 (41)
(41)
Вместо последнего граничного условия при х=L зададим дополнительное условие при х=0: q = q0. Тогда мы получим задачу Коши. Величину q0 можно выбрать произвольно, например, принять в первом приближении равной нулю.
Решив задачу Коши одним из вышеописанных методов, мы определим значение неизвестной величины Т на конце ребра, при х=L. Скорее всего, оно будет отличаться от значения Тос. Сущность метода пристрелки заключается в том, что значение дополнительного начального условия подбирается таким образом, чтобы после решения задачи Коши оказалось выполненным граничное условие на конце рассматриваемого отрезка (в данном случае при x=L). Это действительно напоминает пристрелку при артиллерийской стрельбе, где дополнительному начальному условию можно сопоставить угол наклона ствола орудия, который меняется до тех пор, пока не будет выполнено граничное условие на другом конце – совпадение траектории полета снаряда с точкой местонахождения цели.
Фактически получается, что значение граничного условия на конце отрезка является функцией величины дополнительного начального условия: T½x=L = f(q0). Тогда условие совпадения конечного условия с заданной величиной Тос запишется в виде некоторого нелинейного уравнения:
 ,
,
где функция определяется путем решения задачи Коши. Подбор граничного условия можно, таким образом, проводить с помощью описанных ранее методов решения нелинейных алгебраических уравнений, например, метода половинного деления (что, опять-таки, имеет прозрачную "артиллерийскую" аналогию – взятие цели в "вилку").
3.6. Моделирование процессов, приводящих
к дифференциальным уравнениям в частных производных


 При анализе химико-технологических процессов, нагрева и охлаждения тел и т.п., часто приходится иметь дело с величинами, значения которых меняются от одной точки тела к другой непрерывно. Так, если поместить головку сыра для хранения в холодильник, ее температура будет меняться постепенно. Сначала остынет поверхностный слой, тогда как центральная часть головки будет оставаться теплой. Постепенно охлажденная зона будет занимать все более толстый слой, но в центре головки температура долго будет оставаться более высокой, чем у поверхности. Изменение температуры внутри головки можно представить графиком Т(х), где х – координата, отсчитываемая вдоль диаметра головки. Очевидно, температура является функцией расстояния от центра головки, а также зависит от времени t:
При анализе химико-технологических процессов, нагрева и охлаждения тел и т.п., часто приходится иметь дело с величинами, значения которых меняются от одной точки тела к другой непрерывно. Так, если поместить головку сыра для хранения в холодильник, ее температура будет меняться постепенно. Сначала остынет поверхностный слой, тогда как центральная часть головки будет оставаться теплой. Постепенно охлажденная зона будет занимать все более толстый слой, но в центре головки температура долго будет оставаться более высокой, чем у поверхности. Изменение температуры внутри головки можно представить графиком Т(х), где х – координата, отсчитываемая вдоль диаметра головки. Очевидно, температура является функцией расстояния от центра головки, а также зависит от времени t:


Эта функция непрерывна, т.к. температура в сплошной среде не может измениться скачкообразно. Если вместо симметричной головки взять тело иной формы, температура в нем окажется функцией трех координат и времени:
 (42)
(42)
Такое непрерывное распределение температуры по точкам в сплошной среде называется полем температуры. Поля могут быть образованы и другими величинами – давлением, концентрацией растворённого вещества и т.п.
Бывают векторные поля; например, поле скоростей в жидкости или газе. Если в жидкости движется какое-то тело (например, весло в воде), оно увлекает за собой часть жидкости; в то же время, жидкость вдали от тела остается неподвижной. Вектор скорости изменяется от точки к точке, постепенно уменьшаясь до нуля, так что
 .
.
Такое векторное поле можно представить, как комбинацию трех скалярных полей проекций скорости на оси координат.
3.7. Дифференциальное уравнение теплопроводности
Рассмотрим процесс теплообмена в твердом теле. Количество тепла, передаваемое за некоторое бесконечно малое время dt через бесконечно малый элемент dF поверхности, нормальной к координатной оси Ox, пропорционально dt и dF, а также зависит от скорости изменения температуры в направлении оси Ox – чем быстрее изменяется температура, тем больше передается тепла. В большинстве случаев связь количества передаваемого тепла со скоростью изменения температуры вдоль Ox принимается линейной:

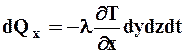 . (43)
. (43)
 |




 Коэффициент пропорциональности l называется коэффициентом теплопроводности; знак "минус" указывает на известный из физики факт – тепло передается в сторону убывания температуры.
Коэффициент пропорциональности l называется коэффициентом теплопроводности; знак "минус" указывает на известный из физики факт – тепло передается в сторону убывания температуры.
Отношение

называется плотностью потока тепла в направлении координаты x (численно величина qx соответствует количеству тепла, передаваемому за 1 сек через 1 м2 поверхности). Аналогично можно записать:

Величины qx, qy, qz можно рассматривать, как компоненты вектора
 ,
,
называемого вектором плотности потока тепла. Он определяет направление переноса тепла через данную точку пространства и количество тепла, переносимого за 1 сек в расчете на 1 м2 площади поверхности, нормальной к этому направлению. Производные температуры по координатам тоже являются компонентами вектора, называемого градиентом температуры:
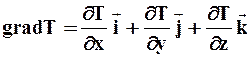 .
.
Для определения градиента температуры необходимо знать вид функции (42), поэтому он является характеристикой температурного поля. Аналогично вводятся градиенты других величин – давления, концентрации и т.п. (существуют и градиенты векторных величин, например, скорости, но их рассмотрение требует применения сложного математического аппарата).
В векторной форме закон теплопроводности записывается:
 .
.
Это соотношение называется законом Фурье. Аналогичный вид имеет так называемый закон Фика, описывающий диффузию какого-либо вещества в сплошной среде:
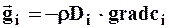 ,
,
где вектор  - вектор плотности потока массы i - компонента смеси веществ (модуль этого вектора показывает, сколько данного вещества проходит за 1 сек через малый элемент поверхности, нормальной к направлению переноса, в расчете на 1 м2 площади поверхности), grad ci – градиент концентрации данного вещества, r - плотность среды, Di – коэффициент диффузии данного вещества.
- вектор плотности потока массы i - компонента смеси веществ (модуль этого вектора показывает, сколько данного вещества проходит за 1 сек через малый элемент поверхности, нормальной к направлению переноса, в расчете на 1 м2 площади поверхности), grad ci – градиент концентрации данного вещества, r - плотность среды, Di – коэффициент диффузии данного вещества.
В силу аналогии законов Фурье и Фика многие закономерности и расчетные формулы теплообмена оказываются справедливыми и для массообмена (диффузии).
Рассмотрим бесконечно малый элемент сплошной среды в виде параллелепипеда с ребрами dx, dy, dz. Через левую грань объема в него поступает количество теплоты dQx, описываемое формулой (43). Одновременно через правую грань из него уходит теплота
 Если температура меняется вдоль оси Ох, значения производных
Если температура меняется вдоль оси Ох, значения производных  на противоположных гранях неодинаковы. В итоге внутри рассматриваемого элемента остается тепло
на противоположных гранях неодинаковы. В итоге внутри рассматриваемого элемента остается тепло
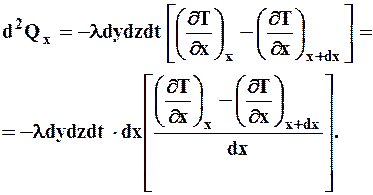
Если dx – бесконечно малая величина (т.е., в конце вывода должен быть совершен предельный переход при  ), выражение в квадратных скобках является второй производной температуры по х (со знаком "минус"); тогда
), выражение в квадратных скобках является второй производной температуры по х (со знаком "минус"); тогда
 .
.
Аналогично можно рассмотреть две другие пары противоположных граней. Тогда общее количество тепла, накопленное в объеме за время dt, равно
 .
.
Накопление тепла вызывает нагрев вещества в объёме:
 ,
,
где  - частный дифференциал температуры.
- частный дифференциал температуры.
Приравняв два выражения для d2Q, получаем
 (44)
(44)
- дифференциальное уравнение теплопроводности. Оно получено в предположении постоянства l и отсутствия внутреннего тепловыделения в сплошной среде (такое тепловыделение может быть обусловлено, например, протеканием химической реакции в веществе или другими физико-химическими процессами). Более общие формы уравнения теплопроводности рассматриваются в литературе по тепломассообмену.
Символом  обозначен так называемый лапласиан температуры (сумма вторых частных производных по координатам). Лапласианы различных величин часто встречаются в дифференциальных уравнениях в частных производных.
обозначен так называемый лапласиан температуры (сумма вторых частных производных по координатам). Лапласианы различных величин часто встречаются в дифференциальных уравнениях в частных производных.
Аналогичным образом (применяя законы физики к бесконечно малым объемам) можно получить и другие дифференциальные уравнения, описывающие процессы в сплошных средах. Примеры таких уравнений:
- уравнение диффузии:
 ;
;
- волновое уравнение (уравнение распространения волн в сплошной среде):
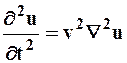 ,
,
где u – величина, волновое колебание которой рассматривается (давление, температура, электрический потенциал и др.), v – скорость распространения волны;
- уравнение Лапласа:
 , (45)
, (45)
описывающее стационарные распределения различных величин (температуры, электростатического потенциала и др.) в сплошной среде.
3.8. Краевые задачи для уравнений в частных производных
Уравнение теплопроводности применимо к анализу распространения тепла в любой системе – от куска сыра до стенки атомного реактора. Поэтому при рассмотрении конкретных задач к уравнению надо добавить описание особенностей задачи, отличающих ее постановку от других задач теплопроводности.
|
|
|
|
|
Дата добавления: 2017-01-13; Просмотров: 433; Нарушение авторских прав?; Мы поможем в написании вашей работы!