Численные методы решения дифференциальных уравнений в частных производных. 1 страница

Сложная структура дифференциальных уравнений в частных производных приводит к тому, что непосредственное решение их возможно только в редких случаях. Обычно прибегают к приближенным численным методам.

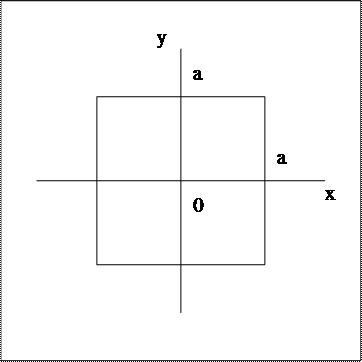
Рассмотрим в качестве простого примера стационарное распределение температуры в двумерной области (например, в тонкой длинной балке квадратного сечения, неравномерно подогреваемой и охлаждаемой с поверхности). Распределение температуры описывается дифференциальным уравнением теплопроводности, в котором отсутствуют производные по времени (процесс стационарный) и по координате z (в длинной балке можно не учитывать изменение температуры по длине). Поскольку l¹0, уравнение (44) приводится к виду

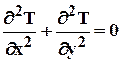, (46)

т.е., к двумерному уравнению Лапласа.

Пусть справа и слева балка подогревается, а сверху и снизу охлаждается, например, по закону:

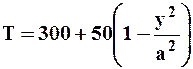(47)

при x=±a,

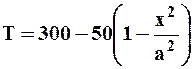(48)

при y=±a.

Выражения (47, 48) являются граничными условиями к уравнению (46).

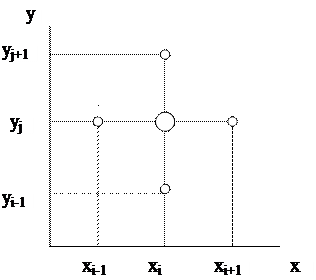Для численного решения дифференциальных уравнений в частных производных чаще всего пользуются различными вариантами метода сеток. Накроем рассматриваемую область сеткой из 2N+1 горизонтальных и 2N+1 вертикальных линий, равноотстоящих друг от друга. Расстояние между соседними линиями составит тогда h = a / N. Точки пересечения линий называются узлами сетки. Будем обозначать линии сетки номерами: i – для вертикальных (соответствующих определенному значению x_i = ih, если номер i изменяется от –N до N) и j – горизонтальных (соответствующих определенным значениям y_j = jh). Тогда узел сетки можно определить по номерам линий, на пересечении которых он лежит.

Рассмотрим один из узлов сетки с номерами i,j.

Обозначим T_i,j=T(x_i,y_j). Аналогично обозначаются значения температуры или ее производных в других узлах сетки. Используя разложение функции T(x,y) в ряд Тейлора, можно записать:

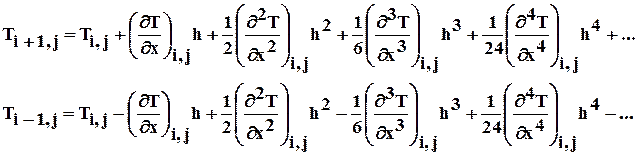
Сложим эти выражения почленно:

.

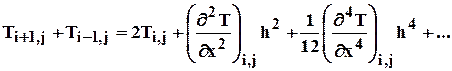Отсюда можно выразить вторую производную:

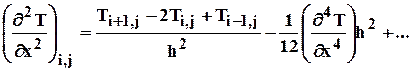(49)

Такой способ получения выражений для производных сеточных функций является более общим, чем графический, представленный в п. 3.4.

Аналогично можно представить и вторую производную температуры по координате y. Подставив приближенные выражения производных в уравнение (48), получим его разностное представление:

,

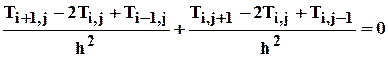или

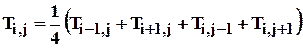. (50)

Записав такие соотношения для каждого узла сетки, получим систему из (N-1)² линейных алгебраических уравнений для нахождения значений температуры в узлах (кроме узлов, лежащих на границах, для которых значения температур определяются граничными условиями (47, 48)).

Решение этой системы можно осуществить различными способами. Наиболее простым (но не самым эффективным) является метод последовательных приближений.

3.9. Оптимизационные модели. Основные понятия и определения

Под оптимизацией понимают процесс выбора наилучшего варианта среди всех возможных. Например, выбор наилучшего варианта конструкции, наилучшего способа раскроя материала, наилучшего режима работы оборудования, наилучшего графика перевозок и т. п.

Если в конкретной задаче обозначить независимые параметры через 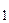x , x 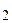, …, x_n, а зависимый параметр через P, то величину P можно представить, как функцию:

P = f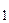(x , x 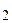, …, x 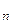). (51)

Процесс оптимизации будет заключаться в том, чтобы найти такие значения аргументов х₁, х₂, …, х_n из области определения функции Р, при которых эта функция достигает наибольшего или наименьшего значения. Функцию Р называют целевой функцией. Параметры 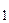x , x 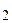, …, x 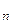в инженерной практике называют проектными параметрами (при решении экономических задач – параметрами плана), область изменения проектных параметров – областью проектирования. Количество n проектных параметров, подлежащих учёту, определяет размерность задач и позволяет разделить их на одномерные (n = 1) и многомерные (n ³ 1).

При решении конкретных задач, как правило, возникает необходимость учитывать дополнительные ограничения, налагаемые на проектные параметры, а также связи между параметрами, отражающие законы природы, сырьевые и материальные ресурсы, спрос и предложения рынка и т.п. Такие задачи называются условными.

Связи и ограничения можно описать в виде ограничений–равенств, ограничений-неравенств, или их совокупности:

Ограничения – равенства: Ограничения – неравенства:

f₁(x₁, x₂, …, x_n) = 0 a₁ 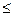q₁(x₁, x₂, …, x_n) 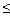b₁

f₂(x₁, x₂, …, x_n) = 0 a₂ 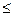q₂(x₁, x₂, …, x_n) 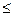b₂ (52)

…………………… ……………………..

f_m(x₁, x₂, …, x_n) = 0 a_k 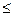q_k(x₁, x₂, …, x_n) 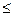b_k

Ограничения сужают область проектирования и иногда позволяют выразить одни проектные параметры через другие, что позволяет уменьшить размерность решаемой задачи и сокращает время, затрачиваемое на решение.

Пример. Необходимо сконструировать контейнер в форме прямоугольного цилиндра, так, чтобы при заданном объёме длина сварных швов была наименьшей.

Целевой функцией (величиной подлежащей оптимизации) является длина швов L. Она зависит от двух параметров: высоты контейнера H и радиуса R, и определяется по формуле:

L = F (H, R) = 4pR + H,

где R, H – проектные параметры. Ограничение на объем банки

V₀ = pR²H

является ограничением-равенством. Воспользуемся им для уменьшения количество проектных параметров. Этого можно достичь, выразив R через V₀ и H, или, выразив H через V₀ и R.

В первом случае:

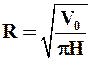и L = F(H) = 4 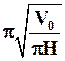+ H.

Во втором:

H = 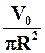и L = F(R) = 4 .

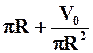Во втором случае оптимизируемая функция оказалась проще, поэтому возьмём её в качестве целевой при естественных ограничениях: H > 0, R > 0.

Теперь можем сформулировать задачу в стандартной форме:

Задача: одномерная.

Проектный параметр: R.

Целевая функция, минимум которой надо найти: L(R)=4pR+V₀/pR² ._.

Основываясь на данном примере, можно заключить, что для разработки математической модели задачи оптимизации необходимо:

· По смысловому содержанию выделить проектные параметры.

· Записать целевую функцию.

· Записать систему ограничений и с помощью ограничений-равенств максимально снизить количество проектных параметров (размерность задачи).

3.10. Схема решения задач оптимизации

Процесс выбора наибольшего или наименьшего значений целевой функции в области проектирования можно провести по схеме:

1. Определить точки максимума или минимума целевой функции внутри области проектирования и вычислить в этих точках её значения.

2. Вычислить значения целевой функции на границе области проектирования.

3. Сравнить полученные значения функции и выбрать среди них требуемое экстремальное.

4. За значения проектных параметров x₁, x₂, …, x_n принять значения, удовлетворяющие выбранному значению целевой функции.

Оценим эту схему с точки зрения практической реализации. Для нахождения максимального или минимального значения функции мы располагаем классическим методом приравнивания к нулю производных, применимость которого распространяется только на достаточно простые, непрерывные и дифференцируемые целевые функции. Получаемая при этом система уравнений:

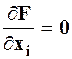, (i = 1, 2, …, n) (53)

подлежит решению. Решение таких систем даже для определения одной точки, подозрительной на экстремум - весьма трудоёмкое мероприятие. А ведь целевая функция может иметь внутри области проектирования несколько экстремумов.

Далее, если граница области проектирования задана аналитическими соотношениями в виде равенств или неравенств, то практически невозможно вычислить значения целевой функции в каждой точке границы. Отсюда следует, что для нахождения экстремумов целевых функций необходимы специальные численные методы.

3.11. Численные методы решения задач

безусловной одномерной оптимизации

Пусть требуется найти экстремум (максимум или минимум) функции одной независимой переменной

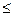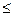y = f(x) при a x b.

Интервал изменения параметра х принято называть интервалом проектирования или интервалом неопределенности.

В дальнейшем условимся:

· рассматривать только поиск минимума целевой функции, поскольку в силу симметричности функции y = f(x) и y = -f(x) относительно оси Ох, минимум функции y = f(x) является максимумом для функции y = -f(x);

· предполагать, что на интервале неопределённости целевая функция унимодальна, т.е. имеет только один экстремум.

Последнее предположение не ограничивает применимость методов оптимизации для целевых функций, имеющих несколько локальных (местных) экстремумов, т.к. найдя локальные экстремумы и, сравнив их, найдем экстремум глобальный (справедливый для всей области проектирования).

Классический метод для функции одной переменной приводит к решению уравнения 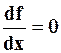. Найти его корни можно:

· для простых уравнений непосредственно: путем выделения переменной x для уравнений вида ax + b = 0; через дискриминант для уравнений квадратных: ax 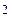+ bx + c = 0 и приводящихся к ним и т.д.;

· для сложных - применением специальных методов, например последовательных приближений, половинного деления (см. выше п. 3.2).

Если же функция y = f(x) или ее производная сложны или имеют разрывы в некоторых точках интервалах [a, b], то применение классического приема затруднительно или невозможно. Численные методы в этих случаях действуют безотказно. Суть этих методов заключается в сужении границ интервала неопределенности (внутри которого заключена искомая точка экстремума) до таких размеров, в пределах которых любая точка x может быть взята в качестве приближенного решения c некоторой, заранее оговорённой точностью. Точность решения, естественно, задается разработчиком либо по длине интервала неопределенности DL, либо по изменению целевой функции DF (см. рисунок), исходя из смыслового содержания решаемой задачи.

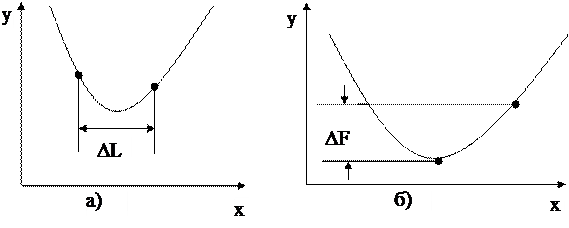Определение погрешности:

а) по длине интервала неопределённости DL;

б) по значениям целевой функции DF.

Условимся задавать точность по длине интервала неопределенности DL.

Наиболее простым для понимания является метод половинного деления. Этот метод сужает интервал на каждом этапе ровно вдвое и требует на каждом шаге вычисления значения функции в двух точках.

Алгоритм метода половинного деления:

1. Определяется первоначальный интервал неопределенности [a,b] (анализом графика или таблицы значений функции F(x).

2. Определяется численное значение производной 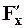в точке c=(a+b)/2, то есть, в середине интервала. Для этого можно использовать приближенное выражение второго порядка точности (25); в качестве шага h берется значение e/2;

3. Если производная положительна, за новый интервал неопределенности принимается [a, c], в противном случае [c, b]. Если производная окажется равной нулю, искомая точка минимума – это точка с.

4. Шаги 2, 3 повторяются до тех пор. пока новый интервал неопределенности не окажется короче, чем допустимая величина погрешности e. Тогда за искомую точку принимается середина последнего найденного интервала.

(Замечание: из выражения (25) видно, что можно не определять производную, а просто поставить условие:

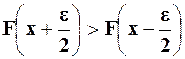
Если оно выполнено, производная положительна, в противном случае – отрицательна).

3.12. Многомерная безусловная оптимизация

Пусть целевая функция зависит от n проектных параметров:

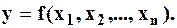
Для простоты изложения условимся отыскивать экстремум целевой функции, зависящей от двух проектных параметров 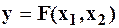. Зададим координаты начальной точки M⁰(x₁₀, x_20). На первом этапе параметр 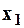зафиксируем, а x₂ будем считать переменным. Целевая функция будет зависеть только от одного параметра. x₂, так что, применив к ней вышеописанный метод решения задач одномерной оптимизации, находим экстремальное значение по этому свободному параметру, то есть, при фиксированном значении параметра x₁=х₁₀. На этом первый шаг заканчиваем. Взяв полученную точку в качестве начальной и, приняв теперь в качестве свободного параметра 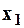, находим экстремум по этому параметру, зафиксировав, соответственно, х₂. В результате получаем конечную точку M 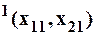первого этапа. Взяв её в качестве стартовой на втором этапе, и, повторив схему движения первого этапа, получим возможность продолжения пути на третьем этапе и т.д. Процесс следует закончить, если для двух соседних этапов: k- го и (k+1)- го выполнятся соотношения

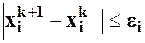для ,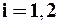

где 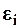-точность вычислений i- го параметра. Впрочем, точность может быть одинаковой по всем параметрам.

3.13. Условная оптимизация при решении инженерных задач

До сих пор мы рассматривали численные методы для задач безусловной оптимизации. На практике довольно часто задача кроме целевой функции предполагает наличие дополнительных условий и становится задачей условной оптимизации. Наиболее простой случай такой оптимизации имеет вид:

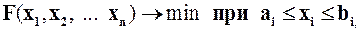
т.е. для каждого проектного параметра введены граничные условия.

Такую задачу можно решить по той же схеме решения, что и для безусловной оптимизации. В том случае, когда значение переменной 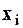на k -ой итерации выходит на (или за) нижнюю границу, т.е. оказывается 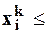а 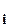, то за минимальное значение 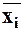принимают а 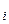и поиск продолжается по остальным переменным. Аналогично осуществляется поиск и для верхней границы.

3.14. Линейное программирование

Мы рассмотрели задачи условной оптимизации, которые могут быть сформулированы при решении инженерных задач. В экономике такой класс задач является предметом изучения раздела науки – математического программирования. Последнее слово появилось в наименовании по той причине, что широкое решение таких задач стало возможным только с появлением электронной вычислительной техники. Совокупность проектных параметров называется планом, а сами параметры – компонентами плана. Ограничений в таких задачах может быть сколько угодно. Самый простой случай ограничений - это когда количество ограничений равно количеству проектных параметров. В этом случае задача имеет единственное решение. Такие задачи практически не представляют интереса, т.к. не предоставляют возможности выбора.

В настоящее время уже выделился определённый класс задач, эффективно решаемых методами математического программирования. Это задачи: распределительные; управления запасами; замены оборудования; упорядочения и согласования; выбора оптимальных режимов движения и др.

Если в решаемой задаче целевая функция и ограничения линейно зависят от проектных параметров, то задача относится к разделу линейного программирования, в противном случае к нелинейному. Мы рассмотрим только задачи линейного программирования.

Рассмотрим пример: Цех располагает четырьмя группами оборудования А, В, С, D и выпускает 2 вида продукции. Количество единиц оборудования и его занятость приведены в таблице. Там же даны величины прибыли, получаемой за счет выпуска единицы продукции каждого вида.

Задача: определить план выпуска продукции каждого вида, обеспечивающий максимальную прибыль.

Группы оборудования	Количество единиц оборудования в группе	Количество единиц оборудования, используемых при выпуске единицы продукции
Вида 1	Вида 2
А
В
С
D
Прибыль		200 руб.	300 руб.

Математическая постановка задачи:

Обозначим через x₁ и x₂ – количество единиц продукции 1-го и 2-го вида соответственно, планируемое к выпуску. Тогда целевая функция выразится:

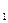L (x ,x 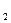) = 200x₁ + 300x_2. ( 54 )

Ограничения, определяющие занятость оборудования по группам:

А: 2x₁ + 2x₂ £ 12 x₁ + x₂ £ 6,

B: x₁ + 2x₂ £ 10 или x₁ + 2x₂ £ 10,

C: 4x₁ + 0x₂ £ 16 x₁ £ 4, ( 55 )

D: 0x₁ + 4x₂ £ 12 x₂ £ 3.

Естественные ограничения:

x₁ ³ 0, x₂ ³ 0. (56)

Требуется определить наибольшее значение целевой функции L(x 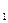, x₂) при ограничениях (55) и (56).

Рассмотрев пример, можем сформулировать задачу линейного программирования в общем виде: необходимо найти наибольшее (наименьшее) значение целевой функции

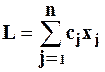(57)

при ограничениях: ресурсных:

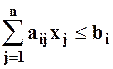, (i = 1, 2, …, m) (58)

и естественных:

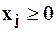, (j = 1, 2, …, n), (59)

где 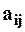- коэффициенты при неизвестных в ограничениях.

В задачах линейного программирования ограничения формируют область допустимых решений.

Если задача имеет только два параметра, то она может быть решена графически. При большем числе параметров для решения надо использовать специальный метод, называемый симплекс – методом.

Проиллюстрируем суть графического метода на примере решения задачи, поставленной выше

1. На плоскости построим систему координат x₁, x₂.

2. Построим область допустимых решений. Из естественных ограничений (47)следует, что она расположена в первой координатной четверти, т.е. выше оси Оx₁ и правее оси Оx₂.

На первом ресурсном ограничении покажем как строится область. Сохранив в ограничении только знак равенства, превращаем это ограничение в уравнение прямой x₁ + x₂ = 6. Строим эту прямую. Она делит плоскость на две полуплоскости: полуплоскость, лежащую выше и полуплоскость лежащую ниже её. Для определения требуемой полуплоскости возьмём любую точку, принадлежащую одной из полуплоскостей, и поставим её координаты в рассматриваемое ограничение – неравенство. Для простоты вычислений возьмём точку начала координат, т.е. точку O(0,0), поставив её координаты в неравенство, получим верное выражение: 0 £ 6. Из этого следует вывод о том, что в область допустимых решений входит полуплоскость, расположенная ниже прямой x₁ + x₂ = 6.

Аналогично определяем полуплоскости, соответствующие остальным ограничениям. Общая часть всех полуплоскостей образует область проектирования OABCD, выделенную на рисунке.

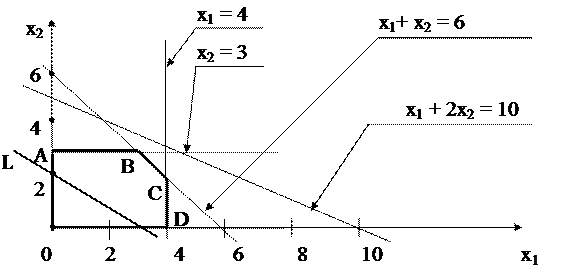Вершинами образованного пятиугольника OABCD являются точки пересечения прямых. Любая точка, принадлежащая этому пятиугольнику, определяет допустимое решение задачи или допустимый план, который может быть выполнен при имеющихся ресурсах.

3. Для нахождения оптимального плана нам необходимо найти такую точку, принадлежащую пятиугольнику, в которой целевая функция достигает наибольшего значения.

Рассмотрим на плоскости x₁x₂ линии уровня этой целевой функции; они представляют семейство прямых линий, параллельных прямой

L = 200x₁ + 300x₂

Зададим значение L таким, чтобы прямая проходила через область допустимых решений. При L = 600 получим прямую 2x₁ + 3x₂ = 6. Построим её. Параллельный перенос этой прямой вверх соответствует возрастанию целевой функции, вниз – убыванию. Строим семейство параллельных прямых до тех пор, пока одна из них не соприкоснется с областью допустимых решений в единственной точке. В нашем случае общей последней точкой является точка В с координатами x₁ = 3 и x₂ = 3, полученная пересечением линий: x₁ + x₂ = 6 и x₁ = 3. Решение x₁ = 3 и x₂ = 3 – единственное из возможных, позволяющих нам получить наибольшую прибыль; при данных значениях параметров она достигнет 1500 руб.

В общем случае предельная прямая может совпасть с одной из границ области допустимых решений. Тогда любая точка этой границы является оптимальным решением, что дает право говорить о бесчисленном множестве решений задачи.

Анализ полученного решения:

1. Анализируя график можно получить информацию о том, какие ресурсные ограничения являются существенными, а какие таковыми не являются. В нашем случае ограничение

x₁ + 2x₂ £ 10

Дата добавления: 2017-01-13