Определение скорости потока на выходе из канала

Закон геометрического обращения воздействия

Запишим уравнение неразрывности или сплошности потока

, (2)

где m – массовый расход газа, кг/с.

Преобразуем (2)

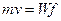. (3)

При дифференцировании получаем

. (4)

Разделив обе части (4) на (3) имеем

. (5)

В рассматриваемом случае (адиабатное изменение состояния газа при его течении) отношение может быть получено из уравнения адиабаты

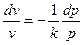. (6)

Поделив уравнение (1) на W­², получим

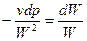. (7)

Совместное решение (5), (6) и (7) дает

. (8)

Скорость звука в среде определяется соотношением

. (9)

В настоящее время при анализе течения газа широко используется число или критерий Маха, представляющий собой отношение скорости потока к скорости звука в том же сечении

.

Если разделить числитель и знаменатель в круглых скобках выражения (8) на а­², то получим

. (10.1)

Используя (6) получим

. (10.2)

Используя (7) получим

. (10.3)

С использованием температуры

. (10.4)

Совокупность выражений (10.1), (10.2), (10.3) и (10.4) является аналитическим выражением закона геометрического обращения воздействия.

Этот закон устанавливает взаимосвязь между геометрией канала (f), параметрами рабочего тела (p, v, T), скоростью потока (W) и режимом течения (M).

Определение скорости потока можно осуществить путем интегрирования уравнения (1) в пределах от входного до выходного сечения канала.

Проинтегрируем уравнение (1)

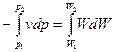
или

. (11)

Решением интеграла в левой части уравнения (11) оказывается возможным, если известна зависимость 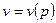. В общем случае можно признать, что изменение состояния газа в процессе течения происходит по закону политропы, т.е.

.

В случае адиабатного течения

. (12)

Подставляя значение v из (12) в (11) и производя интегрирование, получим

. (13)

Уравнение (13) определяет приобретенный газом запас кинетической энергии, который может быть превращен в работу на колесе турбомашины. Поэтому величину, стоящую в левой части уравнения иначе называют располагаемой работой газового потока.

Располагаемая работа – это потенциальная энергия газа, которая может быть преобразована в кинетическую энергию потока при расширении его от давления р₁ до р₂.

Если принять 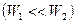, то из уравнения (13) следует, что скорость на выходе из канала будет равна

. (14)

Дата добавления: 2017-01-14