Вывод дифференциального уравнения для нестационарного режима в подвижной среде с внутренними источниками теплоты в декартовой системе координат

ДИФФЕРЕНЦИАЛЬНОЕ УРАВНЕНИЕ ТЕПЛОПРОВОДНОСТИ

ЛЕКЦИЯ 9

Рассмотрим процессы происходящие в подвижной среде с внутренними источниками теплоты (токи Фуко, парообразование, конденсация).

Выделим в подвижной среде элементарный объем в виде прямоугольного параллелепипеда со сторонами dx, dy, dz.

Запишем уравнение теплового баланса для данного случая

,

где – изменение энтальпии;

– подводимое количество теплоты;

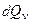– внутреннее изменение теплоты.

Вывод уравнения производим при следующих условиях:

q_v = const(q_v – удельная производительность внутренних источников теплоты).

l = const – коэффициент теплопроводности.

Чтобы построить математическую модель этого объекта надо все параметры увязать в одно уравнение.

Изменение энтальпии

,

где - объем; - изменение температуры во времени.

Определяем подводимое количество теплоты

- входящий поток по направлению оси x.

где - поверхность, через которую проходит тепловой поток по направлению оси x.

- количество теплоты, выходящее из элементарного параллелепипеда в направлении оси x,

где - температурный градиент.

- количество теплоты, аккумулированной элементарным объемом в направлении x.

- результирующее количество теплоты.

Запишем уравнение теплового баланса:

разделим это уравнение на , тогда:

- дифференциальное уравнение второго порядка.

- коэффициент температуропроводности является мерой теплоинерционных свойств материалов. Приводится в таблицах, определяется экспериментально.

Температура обладает полным дифференциалом, значит:

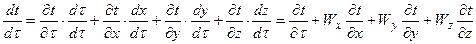
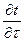- локальная составляющая изменения температуры во времени;

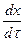- составляющая скорости по оси x;

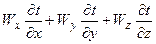- конвективная составляющая изменения температуры.

- дифференциальное уравнение теплопроводности в декартовой системе координат или уравнение Фурье-Кирхгофа для подвижной среды при нестационарном режиме.

Дата добавления: 2017-01-14