
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Ценообразование при опционных сделках
|
|
|
|
Ценой опционного контракта является его премия (а не цена исходного актива), которую уплачивает покупатель (держатель) опциона его продавцу (подписчику) за свое право потребовать исполнения опциона или отказаться от исполнения его в заданных временных границах. Премия устанавливается за единицу биржевого актива. Например, имеем опцион на покупку 100 акций. Рыночная премия составляет 5 руб. за одну акцию. Премия, которую уплачивает покупатель опциона его продавцу, за весь опцион составит: 100 • 5 = 500 руб.
Цена опциона коренным образом отличается от цены при фьючерсных сделках. Цена фьючерса – это цена фондового актива в будущем, а цена опциона – это цена права выбора решения в отношении этого актива. Выбор покупателя опциона будет зависеть от уровня рыночной цены актива на момент возможного исполнения опциона. Если рыночная цена превысит цену исполнения опциона плюс уплаченную премию, то покупателю опциона колл становится выгодно исполнить его, так как прирост цены превысит его затраты (премию). Если этого не произойдет, то покупатель откажется от исполнения опциона и понесет убыток в размере уплаченной премии.
Стоимость опциона складывается из двух составляющих: внутренней стоимости и временной стоимости.
Внутренняя стоимость опциона на покупку (колл) – разница между текущей ценой актива на рынке (ценой спот) и ценой исполнения опционного контракта. Внутренняя стоимость опциона на продажу (пут) – разница между ценой исполнения и ценой спот. Если опцион имеет внутреннюю стоимость (т.е. может быть исполнен с прибылью), его называют «опцион при деньгах». Если опцион не имеет внутренней стоимости, его называют «опцион без денег».
Временная стоимость опциона – разница между его премией и внутренней стоимостью. Временная стоимость тем выше, чем больше времени остается до окончания срока действия опциона. Это объясняется тем, что временная стоимость отражает вероятностный уровень рыночного риска актива опциона. Чем больший временной срок остается до исполнения опциона (или окончания срока его действия), тем выше вероятность того, что может произойти все более крупное отклонение текущей рыночной цены от среднего значения, или что риск, присущий активу, может достичь своих наибольших расчетных значений (или выйти за их границы). Т.е. увеличивается вероятность того, что продавец опциона понесет крупный убыток, который и призвана компенсировать временная составляющая премии.
Обычно опционные контракты заключаются в ситуации, когда внутренняя стоимость отсутствует или не превышает суммы премии. Прейскурант цен на опционный контракт имеет принципиально иной вид, чем прейскурант фьючерсных цен. Прейскурант цен на опцион более сложен, чем прейскурант цен на фьючерсный контракт, т.к. опционов два: колл и пут. Кроме того, в нем задействованы три цены (а не две, как во фьючерсной торговле): рыночная цена акции (спот), цена исполнения опциона и цена самого опциона – его премия.
Из прейскуранта опциона видны закономерности изменения его цены:
– премия по опциону возрастает с отдалением месяца поставки;
– премия по опциону колл уменьшается с увеличением цены исполнения, а премия по опциону пут увеличивается с увеличением цены исполнения;
– премия по опциону колл связана с премией по опциону пут следующим теоретическим равенством для одного и того же актива с одинаковым месяцем исполнения (поставки) и одинаковой ценой исполнения:
С – Р = Цс – Ци / (1 + r)t – d / (1 + r)t0 (13.4.3)
где С – премия по опциону на покупку (колл);
Р– премия по опциону на продажу (пут) с той же датой исполнения, что и у опциона колл;
Цс – текущая рыночная цена акции (цена спот);
Ци – единая цена исполнения опционов колл и пут;
r – безрисковая ставка процента;
d – доход, приносимый ценной бумагой за время действия опциона;
t – время до окончания срока действия опциона;
t0 – время до выплаты дохода по ценной бумаге.
В практике используется несколько математических моделей цены опциона, которые сводятся друг к другу при определенных условиях. Каждая из моделей имеет свою сферу применения, использования, и точность ее расчетов связана с тем, какое время имеется в распоряжении профессионального торговца (трейдера) для принятия рыночного решения. Если это время измеряется секундами или несколькими минутами, то тут не поможет никакая модель, остается полагаться только на опыт торговли и интуицию. Если процесс принятия решения происходит без особой спешки, то используются математические модели, заложенные в компьютерные программы, при этом задается ряд рыночных параметров (процентная ставка и стандартное отклонение уровня риска), чтобы получить достаточно обоснованное значение теоретической премии (цены опциона) и скорректировать его на рыночную ситуацию (учесть соотношение спроса и предложения).
Первой математической моделью цены опциона была модель Блэка-Шоулза (1973 г.). Эта модель для цен опционов колл и пут европейского типа состоит из четырех уравнений:
С = Цс F(d1) – Ци / (1 + r)t F(d2)
Р = Ци / (1 + r)t (1 – F(d2)) – Цс(1 – F(d2)) (13.4.4)
d1 = ((ln(Цс / Ци) + (r + 0,5М2)t / Мt
d2 = d1 – Мt
где С – теоретическая цена (стоимость) опциона на покупку на данный момент времени;
Р – теоретическая цена (стоимость) опциона на продажу на данный момент времени;
Цс – текущая рыночная цена актива (цена спот базовой акции или облигации);
Цн – цена исполнения опциона;
F – значение функции нормального распределения вероятностей для d1 и d2;
r – безрисковая ставка финансирования;
t– время, остающееся до истечения срока действия опциона;
М – стандартное отклонение (волатильность), т.е. годовое стандартное отклонение относительного изменения цены базового актива.
Биноминальная модель оценки стоимости опциона была предложена в 1979 г. Дж. Коксом, С. Россом и М. Рубинштейном и имеет вид:
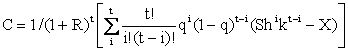 (13.4.5)
(13.4.5)
где С – теоретическая цена (стоимость) опциона на покупку;
R – однодневная безрисковая ставка доходности;
h и k – параметры (числа) случайного изменения цены актива опциона;
t – число интервалов времени, за которые ведется расчет;
S – текущая цена базисного актива;
X – цена исполнения опциона.
Представленные модели применяются в основном для опционов европейского типа. Для опционов американского типа необходимо осуществлять корректировку их результатов в связи с более высоким их риском.
|
|
|
|
|
Дата добавления: 2017-01-14; Просмотров: 710; Нарушение авторских прав?; Мы поможем в написании вашей работы!