Функция распределения

Нормальное распределение (закон Гаусса)

Показательное (экспоненциальное) распределение

Некоторые важные распределения непрерывных случайных величин.

Тема №5.

5.1. Равномерное распределение

Закон равной плотности вероятности имеет место, когда все значения непрерывной случайной величины в некотором конечном ин­тервале () равновозможны.

Плотность вероятности

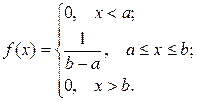
Функция распределения

Моменты: ; ; .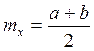

Показательное распределение используется для описания временных интервалов между моментами появления случайных событий в простейшем потоке, подчиняющемся закону Пуассона. Показа­тельное распределениеиграет большую роль в теории случайных про­цессов.

Плотность вероятности .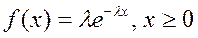

Функция распределения .

Моменты: ; ; .

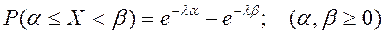Значения функции приведены в табл. 5.1.

Значения функции Таблица 5.1.

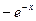
0,01 0,02 0,05 0,09 0,15 0,2 0,3 0,4 0,5 0,6 0,7 0,8 1,0	1,000 0,990 0,980 0,951 0,914 0,861 0,0819 0,741 0,67 0,606 0,549 0,497 0,449 0,368	2,0 2,5 3,0 3,5 4,0 4,5 5,0 5,5 6,0 6,5 6,6 6,7 6,8 7,0	0,135 0,082 0,05 0,030 0,0183 0,0111 0,0067 0,0041 0,0025 0,0015 0,0014 0,0012 0,0011 0,0009

Нормальное распределение возникает в тех случаях, когда складывается много независимых случайных величин , причем эти величины сравнимы по порядку своего влияния на рассеи­вание суммы.

Плотность вероятности

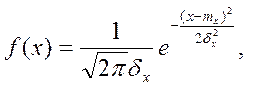
где ; .

Для вычисления F(x) часто используется табулированная функция

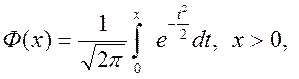
которая называется функцией Лапласа. Функция Лапласа обладает свойствами, которые целесообразно учитывать при расчетах 1) Ф(0) = 0; 2) –Ф(-х) = Ф(х) (нечетная функция); 3) Ф(+¥) = 0,5 и, значит Ф(-¥) = -0,5.

Моменты: ; ; .

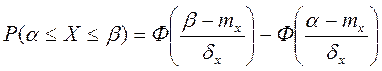Если не принимать во внимание событий, происходящих с веро­ятностями не более 0,0027, то можно практически ограничить диа­пазон возможных значений нормальной случайной величины ; . (правило «трех сигма»). Значения функции приведены в табл. 5.2, 5.3.

Значения плотности стандартного нормального распределения . Таблица 5.2.

0,1 0,2 0,3 0,4 0,5 0,6 0,7 0,8 0,9 1,0 1,1 1,2 1,3 1,4 1,5 1,6 1,7 1,8 1,9 2,0	0,3989 0,3970 0,3910 0,3810 0,3683 0,3521 0,3332 0,3123 0,2897 0,2661 0,2420 0,2179 0,1942 0,1714 0,1497 0,1295 0,1109 0,0941 0,0790 0,0656 0,0540	2,1 2,2 2,3 2,4 2,5 2,6 2,7 2,8 2,9 3,0 3,1 3,2 3,3 3,4 3,5 3,6 3,7 3,8 3,9 4,0	0,0440 0,0355 0,0283 0,0224 0,0175 0,0136 0,0104 0,0079 0,0060 0,0044 0,0033 0,0024 0,0017 0,0012 0,0009 0,0006 0,0004 0,0003 0,0002 0,0001

Значения функции Лапласа . Таблица 5.3

0,1 0,2 0,3 0,4 0,5 0,6 0,7 0,8 0,9 1,0 1,2 1,5	0,00000 0,03983 0,07926 0,11791 0,15542 0,19146 0,22575 0,25804 0,28814 0,31594 0,34134 0,38493 0,43319	2,0 2,5 2,6 2,7 2,8 2,9 3,0 3,5 4,0 4,5 4,6 4,8 5,0	0,47725 0,49379 0,49534 0,49653 0,49744 0,49813 0,49865 0,49977 0,499968 0,499997 0,49999978 0,49999992 0,49999997

Такое распределение имеет самое важное практическое значение.

Дата добавления: 2017-01-14