Геометрическое распределение

Биномиальное распределение

Некоторые важные для практики распределения дискретных случайных величин.

ТЕМА №4.

Задачи для самостоятельного решения.

1. Работают независимо друг от друга 3 устройства. Вероятность нормальной работы 1-го устройства равна 0,8; второго 0,9; третьего 0,8. Построить ряд распределения и функцию распределения для случайной величины х - число работающих нормально устройств.

2. В программе MS Excel подсчитать точечные характеристики заданных случайных величин (рост, вес студентов в группе) - математическое ожидание, дисперсию, среднеквадратическое отклонение, моду, медиану, коэффициент корреляции между величинами.

Формальная модель – производится n независимых опытов, в каждом из которых с вероятностью P происходит случайное событие, X – число появлений события А имеет биноминальное распределение.

Ряд распределения 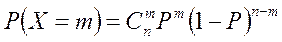, где ; .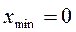

Моменты: ; .

Пример биноминального распределения дан в таблице 4.1.

Таблица 4.1

Биноминальное распределение

N		0,01	0,1	0,5
		0,95099 0,04803 0,00097 0,00001 0,00000 0,00000	0,59049 0,32805 0,07290 0,00810 0,00045 0,00001	0,03125 0,15625 0,31250 0,31250 0,15625 0,03125
		0,73970 0,22415 0,03283 0,00310 0,00021 0,00001 0,00000 - - - - - - - - - - - - - - - - - - - - -	0,04239 0,14130 0,22766 0,23609 0,17707 0,10230 0,04736 0,01804 0,00576 0,00157 0,00037 0,00007 0,00001 0,00000 - - - - - - - - - - - - - -	- - - 0,00000 0,00003 0,00013 0,00055 0,00190 0,00545 0,01332 0,02798 0,05088 0,08055 0,11154 0,13544 0,144446 0,13544 0,11154 0,08055 0,05088 0,02798 0,01332 0,00545 0,00190 0,00055 0,00013 0,00003 0,00000

Биноминальное распределение в общем случае асимметрично. Оно становится тем более симметричным, чем больше n или чем ближе Р к величине 0,5.

Формальная модель – производятся ряд независимых опытов с целью наблюдать событие А (появление А называют "успехом" опыта). При каждой попытке успех достигается с вероятностью Р.

Случайная величина X – число безуспешных попыток (до первой попытки, в которой появляется результат А).

Ряд распределения

.

Моменты: ; ; .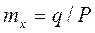

Пример геометрического распределения показан на рис. 4.1 (для случая Р = 0,5).

Рис. 4.1. Геометрическое распределение

Дата добавления: 2017-01-14