Задачи для практических занятий и самостоятельной работы. F-распределение Фишера

F-распределение Фишера

Формальная модель – случайные величины и подчинены нормальному закону распределения с нулевым средним и произвольной дисперсией .

Величины не зависят от 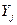. Кроме того, пусть среди 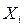имеется , а среди – линейно независимых величин.

Тогда случайная величина

подчинена F -распределению с числами степеней свободы числителя и знаменателя .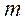

Распределение Фишера находит применение при проверке оценок дисперсий, при статистической проверке вероятностных гипотез о качестве различных моделей случайных процессов.

Пример 5.1. Используя программу MS Excel, построим нормальный закон распределения на интервале (-3;3). Определим функцию распределения и функцию плотности распределения. Для этого воспользуемся стандартной функцией НОРМРАСП (значение; среднее; стандартное отклонение; интегральный). В нашем случае – нормированное нормальное распределение, поэтому среднее равно нулю, а стандартное отклонение - единице. Значит, в ячейке А19 запишем формулу =НОРМРАСП(А18; 0; 1; ИСТИНА), а в ячейке А20 - =НОРМРАСП(А18; 0; 1; ЛОЖЬ). В одной системе координат построим графики функций F(x) и f(x) (рис. 5.1 и 5.2).

Рис. 5.1. Построение таблиц для нормального закона распределения

Рис. 5.2. Графики F(x) и f(x) для нормального закона распределения.

1. Построить графически законы распределения (ряды, плотности вероятностей, функции распределения) для непрерывной случайной величины.

а) нормальное распределение на интервале (-3;3) с шагом 0,1;

б) распределение Стьюдента на том же интервале по формуле =ЕСЛИ(А1<0;(СТЬЮДРАСП(-А1;4;1));(1-СТЬЮДРАСП(А1;4;1));

в) распределение Фишера на интервале (0,1; 40) с шагом 0,5 по формуле =1- FРАСП(А1;4;4);

г) распределение хи-квадрат на интервале (0,5; 40) с шагом 0,5 по формуле 1-ХИ2РАСП(А1;10).

2. Отметить значения, соответствующие математическому ожиданию , моде 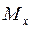, медиане 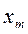и отклонениям от математического ожидания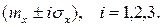

Дата добавления: 2017-01-14