Ошибки 1-го и 2-го рода

Условия	Решения
Принять H0	Принять H1
Справедлива H0	Правильное	α-вероятность ошибки 1 рода
Справедлива H1	β-вероятность ошибки 2 рода	Правильное

7.1.1. Проверка гипотезы о математическом ожидании контролируемого параметра большой партии изделий с нормальным законом распределения и известной дисперсией по выборке малого объема (n₁ = 10)

Гипотеза H₀:

Гипотеза H₁:

Вид выборки: любая – большая, малая.

Закон распределения: нормальный.

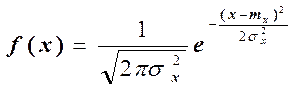, (7.1)

где 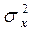известна.

Статистика – формируемая случайная величина с известным законом распределения:

(7.2)

Закон распределения статистики U нормальный, m_u = 0; σ_u = 1.

Условия принятия H0: çU ç< çUкр ç.

Определение величины Uкр показано на рис. 6.1.

Рис. 7.1. Определение критического значения статистики Uкр

Sкр обозначает величину площади.

7.1.2. Проверка гипотезы о математическом ожидании контролируемого параметра большой партии изделий, с нормальным законом распределения и неизвестной дисперсией по выборке малого объема (n1 = 10)

Гипотеза H₀: 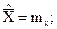(7.3)

Гипотеза H₁:

Вид выборки: любая – большая, малая.

Закон распределения – (1), где неизвестна.

Статистика:

(7.4)

(7.5)

Закон распределения статистики U – распределение Стьюдента с n = (n₁ – 1) степенями свободы.

Условие принятия гипотезы H0: çU ç< çUкр ç.

7.1.3. Проверка гипотезы о математическом ожидании контролируемого параметра большой партии изделий с произвольным законом распределения по выборке большого объема (n1 = 40)

Гипотеза H₀: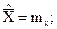

Гипотеза H₁:

Вид выборки: большая.

Закон распределения: произвольный.

Статистика – (7.4), (7.5).

Закон распределения статистики U нормальный закон, m_u= 0; σ_u= 1.

Условия принятия H₀: çU ç< çUкр ç.

Для наглядности можно использовать рис. 7.1.

7.1.4. Проверка гипотезы о средних значениях контролируемого параметра больших партий изделий с нормальным законом распределения и известными дисперсиями по двум малым выборкам (n1 = 10; n2 = 15)

(7.6)

Гипотеза H0:

Гипотеза H1: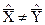

Вид выборки: любая – большая, малая.

Закон распределения – для независимых случайных величин x,y нормальные законы распределения с известными дисперсиями σ_x², σ_y².

Статистика:

Закон распределения статистики U – нормальный закон, m_u=0; σ_u²=1.

Условия принятия H₀: çU ç< çUкр ç.

Для наглядности можно использовать рис. 7.1.

7.1.5. Проверка гипотезы о средних значениях контролируемого параметра двух больших партий изделий с нормальным законом распределения и неизвестными дисперсиями по двум малым выборкам (n1 = 10; n2 = 15)

Гипотеза H₀: , определяемые соотношениями (7.6).

Гипотеза H₁: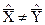

Вид выборки: малая.

Закон распределения – для независимых случайных величин x,y нормальные законы распределения с известными дисперсиями σ_x², σ_y² (в лабораторной работе σ_x²= σ_y²).

Статистика:

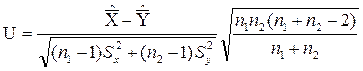(7.7)

(7.8)

(7.9)

Закон распределения статистики U – распределение Стьюдента с n = n₁ + n₂ – 1 степенями свободы.

Условия принятия H₀: çU ç< çUкр ç.

Для иллюстрации можно использовать рис. 7.1.

7.1.6. Проверка гипотезы о средних значениях контролируемого параметра двух больших партий изделий с произвольным законом распределения по выборкам большого объема (n1 = 40; n2 = 40)

Гипотеза H0: , определяемые соотношениями (7.6).

Гипотеза H1:

Вид выборки: большая.

Закон распределения: произвольный.

Статистика: определяется соотношениями (7.7), (7.8), (7.9).

Закон распределения статистики U – нормальный, m_u=0; σ_u²=1.

Условия принятия H0: çU ç< çUкр ç.

Для иллюстрации можно использовать рис. 7.1.

7.1.7. Проверка гипотезы о средних значениях контролируемого параметра двух больших партий изделий с произвольным законом распределения по двум малым выборкам (n1 = 40; n2 = 40)

Гипотеза H₀: , определяемые соотношениями (7.6).

Гипотеза H₁: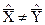

Вид выборки: малая.

Закон распределения: произвольный.

Статистика: Z = x – y; n = n₁ = n₂.

(7.10)

где .

Закон распределения статистики U – распределение Стьюдента с n = n₁ – 1 степенями свободы.

Условия принятия H0: çU ç< çUкр ç.

Для иллюстрации можно использовать рис. 7.1.

7.1.8. Проверка гипотезы о дисперсиях контролируемого параметра двух больших партий изделий с нормальным законом распределения и неизвестными дисперсиями по двум малым выборкам малого объема (n1 = 10; n2 = 10)

Гипотеза H₀: , оценка которых определяется по формулам (7.8), (7.9).

Гипотеза H₁:

Вид выборки: любая – большая, малая.

Закон распределения – нормальное распределение.

Статистика:

1. (основная статистика)

2.

Статистика 2 часто используется при табулировании.

Закон распределения статистики U:

1) F-распределение Фишера с числом степеней свободы числителя K1= (n₁ – 1) и знаменателя K2 = (n₂ – 1).

2) F-распределение Фишера с числом степеней свободы числителя (большей дисперсии) Ki = n_i – 1 и знаменателя Kj = n_j – 1.

Условие принятия H₀:

(см. рис. 7.2.)

K₁ = (n₁ – 1) для числителя,

K₂ = (n₂ – 1) для знаменателя.

Рис.7.2. Определение статистики Uкр для распределения Фишера

7.1.9. Проверка гипотезы о дисперсии контролируемого параметра большой партии изделий с нормальным законом распределения по выборке малого объема (n1 = 10)

Гипотеза H₀: , оценка определяется по формулам (7.8).

Гипотеза H₁:

Вид выборки: любая – большая, малая.

Закон распределения – нормальное распределение.

Статистика:

, (7.11)

где определяется формулой (6.6).

Закон распределения статистики U – χ²-распределение (закон Пирсона) с числом степеней свободы k=n₁-1.

Условие принятия гипотезы H0:

χ₁²<χ²< χ₂² (7.12)

Графическое представление дано на рис. 7.3.

Рис. 7.3. Определение статистики χ²_кр для распределения Пирсона

Дата добавления: 2017-01-14