Задачи для практических занятий и самостоятельной работы. В таблице приведены числа , которые можно рассматривать как реализации независимых нормально распределенных величин с параметрами

В таблице приведены числа , которые можно рассматривать как реализации независимых нормально распределенных величин с параметрами , .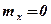

Нормально распределенные случайные числа Таблица 8.4.

№		№		№
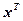
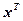
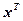
	0,464 0,060 1,486 1,022 1,394 0,906 1,179 -1,501 -0,69 1,372 -0,482 -1,376 -1,010 -0,005 1,393 0,137 -2,256 -0,354 -0,472 -0,555 -0,513 -1,055 -0,488 0,756 0,225 1,678 -0,15 0,598 -0,899 -1,163 2,455 -0,531 -0,634 1,279 0,046 -0,525 0,007 -0,162 -1,618 0,378		-0,057 1,356 -0,918 0,012 -0,911 -0,323 -0,194 0,697 3,521 0,321 0,595 0,769 -0,136 -0,345 0,761 -1,229 -0,561 1,598 -0,725 1,231 -0,068 0,543 0,926 0,571 2,945 0,881 0,971 1,033 -0,511 0,181 -0,486 -,256 1,065 0,147 -0,199 0,296 -1,558 1,375 -1,851 1,974		-0,934 -0,712 0,303 -2,051 -0,736 0,856 -0,212 0,415 -0,121 -0,246 -0,288 0,187 0,785 0,194 -0,258 1,579 1,090 0,448 -0,457 0,96 -0,491 0,219 -0,169 1,096 1,239 1,298 -1,190 -0,963 1,192 0,412 0,161 -0,631 -0,748 -0,218 -1,530 -1,983 0,779 0,313 0,181 -2,574

Для получения нормально распределенных случайных чисел с произвольными значениями и необходимо сделать пересчет по формуле

.

Сформированные последовательности чисел могут использоваться при решении задач по данной теме.

Задача 8.1. Для сформированной таким образом выборки объемом n при известной дисперсии оценить математическое ожидание и построить доверительные пределы (рис. 8.1). Отметить значение, соответствующее "истинному" значению математического ожидания.

Задача 8.2. Для сформированной с помощью (8.10) выборки объе­мом n, "считая" дисперсию неизвестной, оценить математическое ожидание и построить доверительные пределы (аналогично рис. 8.1). Отметить значение соответствующее "истинному" значению ма­тематического ожидания.

Задача 8.3. Для сформированной с помощью (8.10) выборки объе­мом n оценить параметр нормально распределенной генеральной совокупности и определить доверительные пределы. Отметить на до­верительном интервале значение, соответствующее "истинному" значе­нию .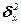

Задача 8.4. Сформировать с помощью (8.9) две выборки объемов n₁, n₂ с различными дисперсиями 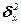, . По методике, изложен­ной в разделе 8.1.4, проверить гипотезу о значениях двух диспер­сий нормального распределения.

Задача 8.5. По данным таблицы 8.3 оценить частоту попадания случайной нормально распределенной величины в заданный достаточно "узкий" интервал Х_i-1:X_i (для таблицы 8.3 величина интервала по­рядка 0,1:0,5). Оценить достоверность оценки вероятности по часто­те для двух случаев, когда "истинное" значение вероятности Р известно (8.7) в когда значение вероятности Р заменяется приближенным значением Р*(8.8).

Задача 8.6. Решить задачи 8.3, 4.4 при известном значении математического ожидания выборки. Отметить повышение точности ис­комых оценок.

Задача 8.7. Используя неравенство Чебышева (4.9), оценить ве­роятность отклонения случайной величины от ее математического ожи­дания. Оце­нить справедливость правила „3 ", согласно которому вероятность (8.9) при α >3 мала.

Дата добавления: 2017-01-14