Нормально распределенные случайные числа

Задачи для практических занятий и самостоятельной работы

8.5.2.1. Произвести обработку наблюдений над системой заданного числа нормально распределенных случайных величин

Имеется система случайных величин . Над системой произведено 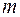независимых наблюдений; результаты этих наблюдений оформлены в виде таблицы, каждая строка которой содержит значений, принятых случайными величинами в одном наблюдении (табл. 8.1).

Таблица 8.1

Таблица наблюдений

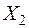
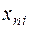
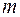
В табл. 8.1 –это значение, принятое величиной в -наблюдении. В табл.8.2 приведены числа , которые можно рассматривать как реализации независимых нормально распределенных величин с параметрами , .

Таблица 8.2

№		№		№
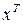
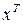
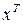
1.	0,464	13.	-1,010	25.	0,225
2.	0,060	14.	-0,005	26.	1,678
3.	1,486	15.	1,393	27.	-0,15
4.	1,022	16.	0,137	28.	0,598
5.	1,394	17.	-2,256	29.	-0,899
6.	0,906	18.	-0,354	30.	-1,163
7.	1,179	19.	-0,472	31.	2,455
8.	-1,501	20.	-0,555	32.	-0,531
9.	-0,69	21.	-0,513	33.	-0,634
10.	1,372	22.	-1,055	34.	1,279
11.	-0,482	23.	-0,488	35.	0,046
12.	-1,376	24.	0,756	36.	-0,525

Для получения нормально распределенных случайных величин с произвольными значениями необходимо сделать пересчет по формуле

.

Для получения коррелированных величин с произвольными значениями необходимо воспользоваться формулой:

,

где 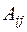– произвольные постоянные коэффициенты.

Требуется найти оценки для числовых характеристик системы: математических ожиданий , элементов ковариационной матрицы { }, элементов нормированной корреляционной матрицы . Оценки для математических ожиданий найдутся как средние арифметические

, ;

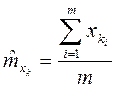несмещенные оценки для дисперсий определятся по формулам

,

для корреляционных моментов – по формулам

.

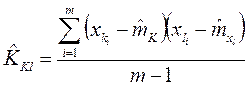По этим данным определяются оценки для элементов нормированной корреляционной матрицы

.

где ; .

8.5.2.2. Определить вероятность попадания случайной точки 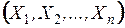в произвольную область -мерного пространства

Вероятность выражается -кратным интегралом по области

.

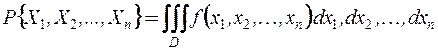В случае, если нормально распределенные случайные величины независимы, а область представляет собой -мерный прямоугольный параллелепипед со сторонами, параллельными координатным осям, то вероятность попадания случайной точки в эту область выражается через функцию Лапласа:

,

где , – координаты границ прямоугольного параллелепипеда в направлении оси 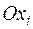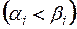; , – математическое ожидание и с.к.о. случайной величины , – функция Лапласа.

8.2.1. Проверка гипотезы о векторе математического ожидания контролируемых параметров большой партии изделий с нормальным законом распределения и известной ковариационной матрицей по выборке малого объема (n1 = 40)

Гипотеза H₀: ,

где – оценка вектора выборочного среднего;

где 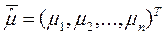– вектор математического ожидания.

Гипотеза Н₁: .

Вид выборки: любая – большая, малая.

Закон распределения: многомерный нормальный закон распределения. Его плотность записывается в виде

,

где , – определитель матрицы K.

, .

Статистика: .

Закон распределения статистики U – -распределение с числом степеней свободы k = n.

Доверительную область можно получать в n-мерном пространстве в виде .

Эта область представляет собой эллипсоид (в двумерном случае – эллипс).

Пример 8.1. По данным контрольных замеров деталей (табл. 8.2), изготовленных на десяти станках (n1 = 10), проверить гипотезу с уровнем значимости 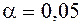о соответствии средних измеряемых параметров деталей X₁, X₂, X₃ (n = 3) контрольным значениям ; ; .

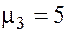Ковариационная матрица считается известной

.

Исходная информация для сравнения параметров Таблица 8.3

Номер изделия	№ станка
X1
X2	1,2	1,2	1,4	1,2	1,2	1,5	1,5	1,3	1,7	1,6
X3	2,1	2,8	3,2	4,5	4,8	4,9	5,5	6,5	8,5

Решение. Исходя из условия задачи, требуется проверить гипотезу H0:

.

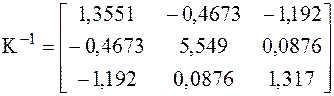Получим неравенство 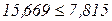, т.е. гипотеза Н₀ отвергается с вероятностью ошибки 0,95.

Таким образом, средние уровни измеряемых параметров деталей не соответствуют контрольным цифрам.

8.2.2. Проверка гипотезы о векторе математического ожидания контролируемых параметров большой партии изделий с нормальным законом распределения и неизвестной ковариационной матрицей по выборке малого объема (n1 = 40)

В отличие от случая 8.5.2 используется статистика Хоттелинга: , где – выборочная ковариационная матрица с элементами , где – значение параметра i в v эксперименте.

Закон распределения статистики – F-распределение с n (для числителя) и n₁ – 1 (для знаменателя) степенями свободы.

Доверительную область можно получить в n-мерном пространстве в виде

.

Это снова эллипсоид.

Пример 8.2. В условиях предыдущего примера решить задачу при неизвестной ковариационной матрице.

Решение. Требуется проверить гипотезу H0: против H1: .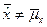

Прежде всего, находим оценку ковариационной матрицы:

.

Значение функции F-распределения .

Получаем соотношение 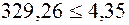, которое говорит о том, что гипотеза Н0 и в этом случае отвергается с вероятностью 0,95.

8.2.3. Проверка гипотезы о средних значениях n контролируемых параметров двух больших партий изделий с нормальным законом распределения и известной ковариационной матрицей по выборке малого объема (n1 = 40; n2 = 40)

Гипотеза H₀: ,

Гипотеза H₁: .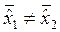

Вид выборки: любая – большая, малая.

Закон распределения: многомерные нормальные законы распределения , .

Статистика: .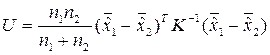

Закон распределения статистики U - 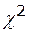-распределение с числом степеней свободы k = n.

Доверительная область определяется условием

.

Эта область представляет собой эллипсоид.

8.2.4. Проверка гипотезы о средних значениях n контролируемых параметров двух больших партий изделий с нормальным законом распределения и неизвестной ковариационной матрицей по выборке малого объема (n1 = 40; n2 = 40)

В отличие от случая 8.5.3 используется статистика:

,

.

Здесь , – ковариационные матрицы партий № 1, № 2.

Закон распределения статистики U – F-распределение с n (для числителя) и (n₁ + n₂ – n – 1) (для знаменателя) степенями свободы.

Доверительную область получим из условия:

.

Как и ранее, это снова эллипсоид.

Подробные таблицы математической статистики можно взять из учебного пособия [1].

8.3. Методические рекомендации к теоретическому разделу 1.

Целесообразно при оценивании параметров распределений формируемых статистик отследить влияние на точность оценок размера выборки. Следует при этом убедиться, что при переходе к интервальному (доверительному) оцениванию точность оценок не повышается. Такой прием (интервальное оценивание) позволяет знать точность и надежность (достоверность) оценки и не более.

Одним из путей повышения точности оценок является увеличение объема выборки n₁.

Дата добавления: 2017-01-14