Определение достоверности уравнения множественной линейной регрессии по критерию Фишера, коэффициенту множественной корреляции

Метод выделения результата АИ

Математические модели связей результатов тестовых испытаний. ОпЕРАТИВНОЕ ОЦЕНИВАНИЕ ПАРАМЕТРОВ МОДЕЛИ регрессии ПРИ НАЛИЧИИ АНОМАЛЬНЫХ РЕЗУЛЬТАТОВ ИЗМЕРЕНИЙ.

Тема №9.

В реальных системах обработки информации оценки вектора регрессионных коэффициентов b для модели

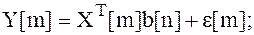
, (9.1.)

где X[m] – вектор наблюдаемых линейно независимых факторов;

b – вектор неизвестных и подлежащих оценке параметров;

e[m] – помеха типа белого шума, приходится проводить в условиях аномальных измерений (АИ) Y(l), l Î ().

В основу алгоритма положен итеративный метод решения на основе метода наименьших модулей. При этом оценка , полученная на основе N результатов измерения, имеет вид

(9.2)

где

(9.3)

(9.4)

где - оценка m-го измерения выходного сигнала.

Начальные значения R[m]=1; соответствуют определению параметров по методу наименьших квадратов (МНК). Далее вычисления оценок по формулам (9.2) – (9.4) проводятся итерационно до тех пор, пока изменения оценок за одну итерацию не достигнут заданной малой величины. При этом наименьший весовой коэффициент R[l] указывает на наиболее грубое l-измерение.

Для оценки достоверности модели применяется критерий Фишера и коэффициент множественной корреляции.

Критерий Фишера:

,

где γ=n – число факторов (C₁ и C₂),

δ=G-n-1, G – число экспериментов (в данном примере 10),

- разброс линии регрессии вокруг среднего значения данных,

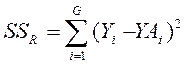- разброс данных вокруг линии.

Если Y_i =YA _i, то R→ ∞.

Далее в Microsoft Excel заполняется следующая таблица:

A	B
	=1-FРасп(А1; n числ; n знам)
...

И по полученным значениям строится график, по которому находится значение F критическое.

Рис. 9.1. Определение значения Fкритич.

С заданной погрешностью, равной 5%, находится значение F критическое.

Если F > F _критич, то модель принимается.

Коэффициент множественной корреляции:

,

где - разброс данных вокруг их среднего значения,

- среднее значение.

Если Y_i =YA _i, то = 0 и KR =1 – точное полное отображение процесса.

Пример. Задана таблица роста и веса 9 девушек.

Рост, x
Вес, y

Составим уравнение регрессии Y=C₀ + C₁*X_1. В программе MS Excel найдем коэффициенты C_i.

C₀ = 13,37, C₁ = 0,31, т.е. уравнение регрессии имеет вид y = 13,37 + 0,31*x1.

Дата добавления: 2017-01-14