Основные сведения из теории

Многомерное нормальное распределение

Тема №8.

Задания для самостоятельной работы

1. Записать значения роста студентов в группе. Это является генеральной совокупностью. Разбить группу на две равные части (выборки). Использовать программу MS Excel.

2. Проверить гипотезу о математическом ожидании контролируемого параметра большой партии изделий с нормальным законом распределения и известной дисперсией по выборке малого объема (n₁ = 10).

3. Проверить гипотезу о математическом ожидании контролируемого параметра большой партии изделий, с нормальным законом распределения и неизвестнойдисперсией по выборке малого объема (n₁ = 10).

4. Проверка гипотезы о средних значениях контролируемого параметра больших партий изделий с нормальным законом распределения и известными дисперсиями по двум малым выборкам (n₁ = 10; n₂ = 15).

5. Для проверки гипотез о двух генеральных совокупностей взять значения роста студентов других групп.

Методы математической статистики. Варианты многомерного статистического контроля

Рассмотрим нормальное распределение для системы произвольного числа случайных величин – вектора в -мерном пространстве. Его плотность записывается в виде:

, (8.1)

где

, (8.2)

. (8.3)

В силу симметрии ковариационной матрицы (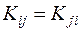) обратная ковариационная матрица также обладает свойством симметрии

. (8.6)

Если нормально распределенные случайные величины независимы (некоррелированы) и при этом , , то их плотность распределения может быть записана в виде:

, (8.7)

которая называется канонической (простейшей) формой нормального закона системы случайных величин .

Для наглядного представления плотности распределения можно получить уравнение -мерного гиперэллипсоида из условия

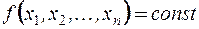, (8.8)

или для случая (8.7)можно записать

(8.9)

При получаем уравнение эллипса равной плотности в декартовой прямоугольной системе координат на плоскости 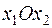(рис.5.1):

(8.10)

Центр этого эллипса находится в начале координат, его полуоси равны: ; .

Рис.8.1. Уравнение эллипса равной плотности

При 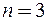получим уравнение эллипсоида равной плотности в декартовой прямоугольной системе координат в пространстве трех измерений (рис.8.2):

(8.11)

Центр этого эллипсоида находится в начале координат, его полуоси равны: ; ; .

Рис. 8.2. Уравнение эллипсоида равной плотности

Дата добавления: 2017-01-14