Понятие множества

Примеры

Неотчуждаемые права и свободы человека и другие нема­териальные блага защищаются гражданским законодатель­ством, если иное не предусмотрено законом (ст. 2 ГК РФ).

Риск случайной гибели или случайного повреждения иму­щества несет его собственник, если иное не предусмотрено законом или договором (ст. 211 ГК РФ).

Наряду с логикой высказываний основу математической логики составляет логика предикатов — логика свойств и от­ношений. Например, "быть юридическим лицом", "иметь пра­во", "нести обязанность", "правонарушение" и др.

Предикатом — свойством некоторого множества называ­ется функция, определенная на этом множестве и принимаю­щая значения "истина" или "ложь".

Рис. 12. Матрица предиката Пр (Х) = "X есть простое число"

Сверху в таблице последовательно записаны натураль­ные числа, снизу стоит буква "и" для тех чисел, которые яв­ляются простыми, и "л" для тех, которые этим свойством не обладают. Аналогично свойство "быть четным числом" пред­ставится следующей таблицей (матрицей):

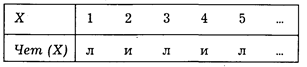
Рис. 13. Матрица предиката Чет (X) = "X есть четное число"

Вообще произвольную таблицу подобного вида можно рассматривать как представление некоторого предиката-свой­ства, определенного на множестве натуральных чисел. Рассмотрим предикат Х — гражданин России.*

* Х в данном случае — переменная величина, взамен которой можно подставлять конкретное имя.

Он определен на множестве всех субъектов, находящихся на территории РФ. Однако для лиц, имеющих паспорт граж­данина РФ, он будет истинным, а для иностранных граждан — ложным.

Рассмотрим теперь пример двухместного предиката:

Субъект Х имеет право совершить действие d.

Здесь имеется отношение между двумя переменными: Х и d. Данный двухместный предикат определен на множестве субъектов и множестве всевозможных действий (d). Он может быть истинным или ложным — в зависимости от того, какие конкретные субъекты и действия подставлены вместо пере­менных.

В логике предикатов наряду с операциями логики выска­зываний важную роль играют кванторы: " s — квантор общно­сти ("все s "); $ s — квантор существования ("некоторые s ").

Логика предиката предоставляет возможность эффектив­но записывать содержание правовых норм с выявлением их внутренней структуры. Так, общие обязывающие и управомочивающие правовые нормы могут быть записаны на языке логики предиката в следующем виде:

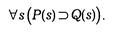
Пример. Если субъект s обладает юридическим свойством Р (является юридическим лицом), то он обязан совершить дей­ствие Q.

Соответственно запретительные нормы имеют общую струк­туру:

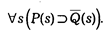
В данном случае s — субъект нормы.

§ 5. Право и законы логики норм

Математическая логика, будучи полезным инструментом исследования и моделирования правовой нормы, недостаточна для описания всех сложных отношений в структуре права. Пра­вовые нормы являются разновидностью нормативных суждений.

Суждения "следователь предъявляет обвинение" и "сле­дователь обязан предъявить обвинение" серьезно отличаются логической формой: первое описывает некоторое состояние и может быть истинным или ложным, второе предписывает не­которое поведение и стоит вне категории истинности или лож­ности.

В нормативных суждениях оценивается характер тех свя­зей, которые содержатся в их внутренней структуре.

Правовые нормы относятся к числу модальных норматив­ных суждений. В их внутренней структуре отражаются такие модальности, как "иметь право", "нести обязанность", "зап­рещено".*

* Модальная логика — это логическая система, изучающая структуру рас­суждений, в состав которых входят модальности (модальные операторы): "необходимо", "возможно", "действительно", "случайно" и их отрицания.

Нормативными операторами будем называть следующие символы:

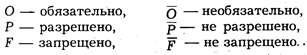
Будучи применен к конкретному высказыванию (d — дей­ствие), нормативный оператор преобразовывает его в модаль­ное суждение:

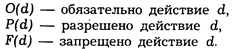
Нормативные операторы представляют собой аналог по­нятия ложности и истинности в обычной индикативной логике.

Следует подчеркнуть относительный характер операторов: то, что разрешено и допустимо в одной нормативной ситуации, может быть запрещено и недопустимо в другой (например, для другого субъекта права). В соответствии с этим в абсолютной нор­мативной логике нормативные операторы рассматриваются при максимальном абстрагировании от условий их применения. В от­носительной нормативной логике свойства нормативных опера­торов рассматриваются уже с учетом условий их действия.

Действие может иметь и положительную, и отрицатель­ную форму. Например, выполнение — невыполнение; соблю­дение — несоблюдение; согласие — несогласие. В дальнейшем отрицательная форма действия будет обозначаться .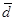

Применение нормативных операторов открывает возмож­ность уточнить математическую модель структуры правовой нормы. Такое уточнение достигается путем указания на юри­дический тип данной правовой нормы.

В целях отображения в структуре правовой нормы мо­дальных связей будем применять следующие обозначения для трех классических типов норм права:

N_P — разрешительные нормы,

n_о — обязывающие нормы,

N_F — запрещающие нормы.

В новой записи структура обязывающих норм будет выг­лядеть так:

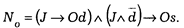
В этом выражении приняты следующие обозначения:

Od — обязательно действие d;

J Ù d — при наличии гипотезы J действие d не совершено;

Os — при наличии предписания и его нарушении обяза­тельно наступление санкции s.

Бесспорно, применение нормативных операторов дает воз­можность промоделировать некоторые аспекты структуры пра­вовой нормы и права в целом. Эти операторы весьма полезны для углубленного изучения правовых структур. Они могут эф­фективно использоваться в практике правотворческой деятель­ности.

При создании экспертных систем приведенные модели целесообразно ввести в память ЭВМ, снабдив их примерами (что может быть полезным для необученного пользования).

Нормативная логика строится как формальная аксиоматичес­кая теория со своими аксиомами, теоремами и правилами вывода.

Далеко не все они имеют значение для правовой инфор­матики. Приведем лишь некоторые из них:

Указанные теоремы представляют собой символическую запись следующих утверждений:

если действие нормативно обязательно в данной системе норм, то оно допустима;

если действие нормативно запрещено, то оно не может быть обязательным;

если действие не запрещено, то оно допустимо (принцип: разрешено все, что не запрещено);

из отсутствия обязанности выполнить действие следует его допустимость.

Некоторые из этих высказываний, будучи переведены на юридический язык, представляют собой уже некоторый логи­ко-юридический принцип.

Логика норм содержит значительное число эквивалентностей, т.е. таких логических выражений, которые сводят зна­чение одного нормативного оператора к значению другого нор­мативного оператора.

Приведем некоторые наиболее важные соотношения:*

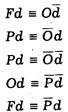
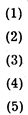
* Символ º означает отношения эквивалентности.

Применение нормативных операторов дает возможность уточнить некоторые положения, связанные с построением не­противоречивой системы правовых норм.*

* Конституция РФ содержит до 10 различных норм, посвященных про­блеме непротиворечивости закона. Главной из них является ст. 15, в со­ответствии с которой правовые акты не должны противоречить Консти­туции РФ.

Закон непротиворечия — один из четырех основных зако­нов формальной логики, который можно выразить следующим образом: не могут быть одновременно истинными две проти­воположные мысли об одном и том же предмете, взятом в одно и то же время в одном и том же отношении. В математи­ческой логике он выражается формулой:

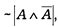
где А обозначает любое высказывание.

Закон непротиворечия не имеет в сфере права практи­ческого значения, ибо он рассчитан на простейшие случаи.

В нормативной логике сформулированы более содержа­тельные требования к непротиворечивости нормативных тек­стов.

Система нормативных высказываний должна быть непро­тиворечива. Противоречивые команды не могут быть выпол­нены. Этот принцип содержится в нескольких нормативных выражениях:*

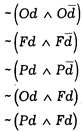
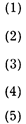
* Символ ~ означает отрицание.

Выражение (1) означает: положения "данное действие обязательно" и "обязательно действие, противоположное дан­ному" (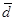), не могут быть одновременно верными.

Выражение (2): никакое действие не может быть одно­временно запрещенным и не запрещенным.

Выражение (3): никакое действие не может быть одно­временно разрешенным и неразрешенным.

Легко понять и смысл соотношений (4) и (5).

§ 6. Математический аппарат

Математический аппарат правовой информатики — это совокупность средств, которыми количественно описываются категории права. В рамках данной работы нет никакой возмож­ности рассмотреть все математические средства. Они обшир­ны и разнообразны. Остановимся на основных.

Множеством принято называть вполне определенную со­вокупность предметов (объектов), которые являются элемен­тами множества. Рассматриваемое понятие (как и понятие фун­кции) лежит в основе всех разделов математики.

Примером множества могут служить следующие явления из области права:

множество правовых норм;

множествоорганов государства;

множество отраслей права;

множество компьютеров, установленных в данной орга­низации;

множество отпечатков пальцев в криминалистике;

множество субъектов федерации;

множество версий при расследовании преступления и т. д.

Множество, все элементы которого изолированы друг от друга, называется дискретным. Для измерения степени их изолированности вводится понятие расстояния между элемен­тами.

Всякое дискретное множество счетно, т. е. его элементы можно пронумеровать целыми числами.

Понятие дискретного множества чрезвычайно важно для информатики, поскольку лежит в основе разделения всех ус­тройств и систем обработки информации на два базовых клас­са — дискретные (цифровые) и непрерывные (аналоговые).*

* Типичный пример дискретного устройства — ЭВМ, состояние памяти которой представляется последовательностью двоичных цифр.

Дата добавления: 2017-02-01