
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Нечеткие множества
|
|
|
|
Операции над множествами
Подобно тому как из двух произвольных чисел с помощью арифметических операций можно получить некоторое другое число, из двух множеств можно сконструировать некоторое другое множество.
Существуют следующие операции над множествами: объединение (образование суммы) и пересечение. Для обозначения этих операций вводятся символы:
È (объединение), Ç (пересечение).
Объединением (суммой) двух множеств А и В называется множество А È В всех элементов, принадлежащих или множеству А, или множеству В, или обоим сразу.
Пересечением двух множеств А и В называется множество А Ç В всех элементов, принадлежащих множеству А и множеству В.
Таким образом:
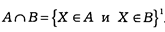
1 Символ Î означает операцию включения Х в состав другого множества.
Американский математик иранского происхождения Лотфи Заде разработал теорию нечетких множеств. Он исходил из того, что человеческому мышлению присуща такая черта, как оперирование размытыми понятиями и образами.
Примерами нечетких множеств являются: "высокий", "хороший", "грамотный", "срочность", "систематичность" и др. В области права наличие нечетких множеств подмечено уже давно. Они получили наименование оценочных понятий. Типичными примерами оценочных понятий являются термины "существенный вред", "исключительный цинизм", "ведущая профессия", "крупный размер", "тяжкие последствия" и др.
С точки зрения требований законодательной техники необходимо превращать нечеткие понятия в четкие.*
* Преступление — это пример нечеткого множества. Состав преступления — это уже четкое множество (понятие), характеризующееся строгими формальными рамками.
Л. Заде ввел в математику понятие лингвистической переменной. Он определял ее как переменную, значения которой суть слова и предложения некоторого естественного или искусственного языка. Например, значениями понятия "скорость" могут быть: "медленная", "умеренная", "большая" и т. д.
Л. Заде нашел способ математически корректного описания свойств нечетких множеств. Сама "нечеткость" обусловлена заданием множества с помощью "лингвистической переменной", т. е. слов или предложений естественного (или искусственного) языка.
Первый шаг заключается в нахождении "всех значений нечеткой переменной.
Степень принадлежности Х Î А элемента нечетному множеству А характеризуется функцией принадлежности:
RA (X).
Данная функция принимает значения между 0 и 1.
Возможно введение так называемых лингвистических вероятностей, которые имеют следующие значения: "правдоподобно", "очень правдоподобно", "неправдоподобно", "чрезвычайно правдоподобно", "весьма правдоподобно" "вероятно", "невероятно", "более или менее вероятно", "маловероятно" и т. д. Для них в качестве базовой используется числовая переменная, принимающая значения на отрезке [0,1], а правила оперирования с такими вероятностями определяются с помощью операций над нечеткими множествами.
|
|
|
|
|
Дата добавления: 2017-02-01; Просмотров: 73; Нарушение авторских прав?; Мы поможем в написании вашей работы!