Показывать уравнение на диаграмме

Решение

Введение

Высшего образования

«Финансовый университет при Правительстве Российской Федерации»

(Финуниверситет)

Смоленский филиал Финуниверситета

Кафедра Математики и информатики

КОМПЬЮТЕРНЫЙ ПРАКТИКУМ

по дисциплине

ЭКОНОМЕТРИКА

Интерактивное занятие

для студентов третьего курса

направления 38.03.01 «Экономика»

(программа подготовки бакалавров)

Заочная форма обучения

2015 г.
Данное интерактивное практическое занятие на ПК имеет следующие цели:

· формирование у студентов умения самостоятельно осуществлять построение в среде EXCEL моделей парной и множественной регрессии и применять их для анализа и прогнозирования экономических процессов;

· проверка степени усвоения студентами лекционного материала по теме парной и множественной регрессии и применение полученных знаний для решения практических задач;

· формирование у студентов убежденности в необходимости освоения данной дисциплины с целью дальнейшего использования приобретенных знаний в практической деятельности.

Задачи занятия:

· формирование у студентов теоретических знаний по вопросам выбора факторных признаков и уяснение основных этапов построения моделей парной и множественной регрессии;

· получение студентами практических навыков при определении параметров регрессионных моделей;

· получение теоретических знаний и практических навыков при оценке качества уравнений регрессии;

· уяснение связи проблемы спецификации модели с ее качеством и возможностью использования для прогнозирования;

· получение студентами практических навыков для выполнения лабораторной и контрольной работ по темам парной и множественной регрессии.

Одним из главных направлений эконометрического анализа является построение моделей парной и множественной регрессий, обладающих высоким качеством, с целью дальнейшего их использования для анализа и прогнозирования развития экономических процессов. Эта проблема в значительной степени зависит от правильной спецификации модели, которая в дальнейшем определяет все свойства теоретической модели и возможность ее использования для построения прогнозов.

Построение регрессионной модели является творческим процессом, опирающимся на серьезные знания в области экономической теории, макро- и микроэкономики, эконометрического анализа и должно быть индивидуально в каждой конкретной ситуации.

Данный компьютерный практикум поможет студентам получить практические навыки по типовой процедуре построения моделей парной и множественной регрессии, выбору факторных признаков, оценке параметров и качеству моделей, построению прогнозов экономических процессов.

Компьютерный практикум состоит из трех заданий:

- в первой задаче по теме «Парная регрессия» студентам предлагается познакомиться с особенностями построения простейших однофакторных (линейных и нелинейных) регрессионных моделей, уяснить основные направления оценки качества моделей парной регрессии и использования их для целей прогнозирования экономических процессов.

Эти знания, несомненно, помогут студентам при освоении следующей темы, касающейся построения, анализа качества и прогнозирования по модели множественной регрессии.

- во второй задаче изложена типовая процедура выбора ведущего фактора из множества факторных признаков и построения линейной модели парной регрессии с целью дальнейшего расчета характеристик модели и определения прогноза результативного признака;

- в третьей задаче по теме «Множественная регрессия» рассмотрены основные этапы спецификации модели множественной регрессии, такие как, определение наличия и устранение мультиколлинеарности, расчет параметров и различных характеристик качества модели и построение прогнозов признаков.

Компьютерный практикум выполняется с использованием программных продуктов EXCEL и SPSS.

Необходимо также отметить важность освоения тем «Парная регрессия» и «Множественная регрессия» ввиду возможности и целесообразности использования практических аспектов данных тем при написании студентами выпускных квалификационных работ, а также в своей практической деятельности.

Задача 1

В качестве показателей, характеризующих результаты финансово-хозяйственной деятельности предприятия, могут быть выбраны:

· Объем выпуска продукции (Y, млн.руб.)

· Объем капиталовложений (X, млн.руб.)

Требуется:

1. Для характеристики зависимости объема выпуска продукции от объема капиталовложений построить следующие модели:

· Линейную;

· Экспоненциальную;

· Гиперболическую.

2. Результаты расчетов отразить на графике.

3. Выбрать лучшую по качеству модель. Ответ обосновать.

Y
X

I. Для построения модели линейной парной регрессии y=a+b*x
воспользуемся встроенной статистической функцией ЛИНЕЙН.

Для этого необходимо:

1) Создайте новый лист Excel (щелчок правой кнопкой на рабочем столе=>Создать=>Лист Microsoft Excel)

2) Введите исходные данные в соответствии с вариантом

Рис.1. Ввод исходных данных

3) Выделите область пустых ячеек 5×2 (5 строк, 2 столбца)

4) Выберите в главном меню Вставка =>Функция

5) В меню Категория выберите Статистические в окне выбора функций – функцию ЛИНЕЙН, нажмите OK (Рис.2)

Рис.2. Окно выбора линейной функции

6) Заполните аргументы функции

Ø Значения Y- диапазон, содержащий значения результативного признака (нажать кнопку в правой части соответствующей ячейки и выделить нужный диапазон A2:A8)

Ø Значения X – диапазон, содержащий данные факторов независимого признака (аналогично B2:B8)

Ø Константа=1

Ø Статистика=1 (см.рис.3)

Рис.3. Окно аргументов функции “Линейн”

7) В левой верхней ячейке появится первый элемент итоговой таблицы. Чтобы раскрыть всю таблицу нажмите F2, а затем комбинацию клавиш <CTRL>+<SHIFT>+<ENTER>.

Дополнительная регрессионная статистика выводится в следующем порядке

Значение коэффициента b	Значение коэффициента a
Среднеквадратическое отклонение b	Среднеквадратическое отклонение a
Коэффициент детерминации R^2	Среднеквадратическое отклонение y
F-статистика	Число степеней свободы
Регрессионная сумма квадратов	Остаточная сумма квадратов

Рис.4. Результаты построения линейной модели

В соответствии с полученными результатами можно записать уравнение линейной регрессии:

y=18,8683+0,79693*x

II. Для вычисления параметров экспоненциальной кривой y=α*β^x воспользуйтесь встроенной статистической функцией ЛГРФПРИБЛ. Порядок вычислений аналогичен применению предыдущей функции. Результаты показаны на рис.5

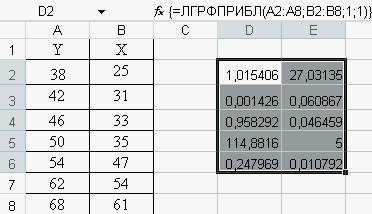
Рис.5. Результаты построения экспоненциальной модели

В соответствии с полученными результатами можно записать уравнение:

y=27,03135*

III. Для построения гиперболической функции воспользуйтесь функцией ЛИНЕЙН, взяв в качестве факторного признака величину 1/X. Для этого в столбце С в ячейке С1 записать название столбца “1/X”, а в ячейку С2 ввести формулу =1/B2, после чего, выделив ячейку С2, навести курсор мыши в правый нижний угол ячейки (появится крестик) нажать левую кнопку и, не отпуская, растянуть выделенную ячейку мышкой до ячейки С8 включительно. Затем воспользоваться уже известной функцией Линейн, взяв в качестве параметра Известные_значения_x диапазон С2:С8. Результаты представлены на рис. 6.

Рис.6. Результат построения гиперболической функции

Запишем уравнение гиперболической функции:

y=84,31121-1228,79/x

IV. Отразите полученные результаты расчетов на графике.

Для этого выполните следующую последовательность действий:

1. Выберите в меню Вставка->Диаграмма, Тип-Точечная. ( рисунок 7)

Рис.7 Выбор типа диаграммы

2. Введите диапазон входных данных (рисунок 8)

Рис.8. Выбор источника данных для диаграммы

3. Оформите вид полученного графика (подписи осей, название графика, и т.д.)

4. Выберите место отображения графика (в имеющемся).

5. Добавьте линию тренда:

- выделите полученную диаграмму и выберите на панели управления
Диаграмма->Добавить линию тренда;

- выбираем Тип-Линейная;

- в закладке Параметры ставим галочки:

Дата добавления: 2017-02-01